If O is the centroid and AD, BE and CF are the three medians of ΔABC with an area of 96cm2 then the area of ΔBOD in cm2 is
8
12
16
24
The correct Answer is:C
To find the area of triangle BOD when O is the centroid of triangle ABC, we can follow these steps:
1. Understand the Properties of the Centroid: The centroid (O) of a triangle divides it into six smaller triangles of equal area when medians are drawn from each vertex to the midpoint of the opposite side.
2. Identify the Area of Triangle ABC: We are given that the area of triangle ABC is 96 cm².
3. Calculate the Area of Triangle BOD: Since the centroid divides triangle ABC into six smaller triangles of equal area, the area of triangle BOD will be one-sixth of the area of triangle ABC.
Area of △BOD=Area of △ABC6
4. Substitute the Given Area: Now, substitute the area of triangle ABC into the equation.
Area of △BOD=96 cm26
5. Perform the Division:
Area of △BOD=16 cm2
Final Answer:
The area of triangle BOD is 16 cm².
---
The area of triangle BOD is 16 cm².
Topper's Solved these Questions
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - III
21 Videos
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV
169 Videos
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself
28 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
- MISCELLANEOUSBOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI
15 Videos
Similar Questions
Knowledge Check
In a ΔABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of ΔABC=72cm2
A12 cm2B16cm2C24cm2D8cm2O is centroid of ΔABC and AD, BE, CF are its three medians. If area of ΔAOE is 15 cm2, then area of quadrilateral BDOF is -
A20 cm2B30 cm2C40 cm2D25 cm2In a ΔABC,AD,BE and CF are three medians. The perimeter of ΔABC is always.
Aequal to (¯¯¯¯¯¯AB+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF)Bgreater than (¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF)Cless than (¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF)DNone of these
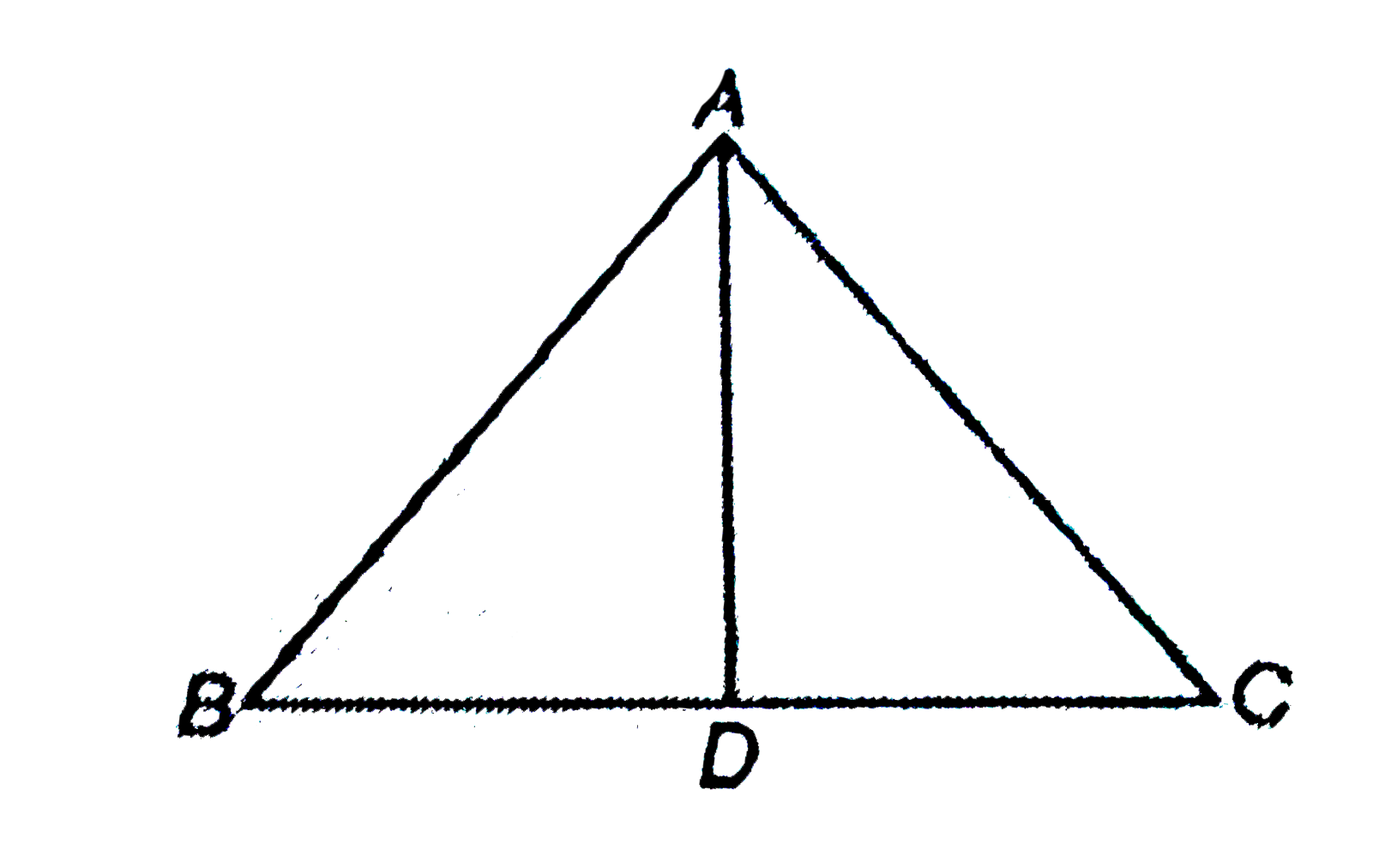
In the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
View SolutionIn a Δ ABC , DE||BC if DE=23 BC and area of ΔABC =81cm2 find the area of ΔADE
View SolutionThree medians AD, BE and CF of ΔABC intersect at G. The area of ΔABC is 36 sq. cm. Then the area of ΔCGE is
View SolutionThree medians AD, BE and CF of ΔABC intersect at G. If area of ΔABC is 36 sq cm, then the area of ΔCGE is
View SolutionIn triangle ABC, AD, BE and CF are the medians intersecting at point G and area of triangle ABC is 156cm2. What is the area (in cm2) of triangle FGE ?
View Solution