Question

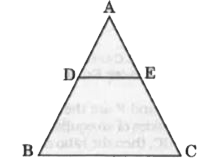
D and E are points on sides AB and AC of $\Delta ABC$. DE is parallel to BC. If AD : DB = 1 : 2 and area of $\Delta ABC$ is 45 sq. cm., what is the area (in sq. cm.) of quadrilateral BDEC ?

Options

A. 20
B. 40
C. 15
D. 30

Answer

B

Explanation

To find the area of quadrilateral BDEC in triangle ABC, we can follow these steps:

Step 1: Understand the given information
We have triangle ABC with points D and E on sides AB and AC respectively. The line segment DE is parallel to side BC. We are given that the ratio AD:DB = 1:2 and the area of triangle ABC is 45 sq. cm.

Step 2: Determine the ratio of the segments
Since AD:DB = 1:2, we can denote the lengths as follows:
- Let AD = 1x
- Let DB = 2x

Thus, the total length of AB (AD + DB) is:
\( AB = AD + DB = 1x + 2x = 3x \)

Step 3: Use the properties of similar triangles
Since DE is parallel to BC, triangles ADE and ABC are similar. The ratio of their areas is equal to the square of the ratio of their corresponding sides.

The ratio of the sides AD to AB is:
\( \frac{AD}{AB} = \frac{1x}{3x} = \frac{1}{3} \)

Step 4: Calculate the area of triangle ADE
The area of triangle ADE can be calculated using the square of the ratio of the sides:
\( \frac{\text{Area of } \triangle ADE}{\text{Area of } \triangle ABC} = \left(\frac{AD}{AB}\right)^2 = \left(\frac{1}{3}\right)^2 = \frac{1}{9} \)

Let the area of triangle ADE be denoted as Area(ADE). We know the area of triangle ABC is 45 sq. cm:
\( \frac{\text{Area of } \triangle ADE}{45} = \frac{1}{9} \)

Thus,
\( \text{Area of } \triangle ADE = 45 \times \frac{1}{9} = 5 \text{ sq. cm} \)

Step 5: Calculate the area of quadrilateral BDEC
To find the area of quadrilateral BDEC, we subtract the area of triangle ADE from the area of triangle ABC:
\( \text{Area of quadrilateral BDEC} = \text{Area of } \triangle ABC - \text{Area of } \triangle ADE \)
\( \text{Area of quadrilateral BDEC} = 45 - 5 = 40 \text{ sq. cm} \)

Final Answer
The area of quadrilateral BDEC is 40 sq. cm.

---