At the foot of a mountain the elevation of its summit is 45∘. After ascending 600 meter towards the mountain, upon an incline of 30∘, the elevation changes to 60∘. Find the height of the mountain.
The correct Answer is:300(1+√3) meter
To solve the problem step by step, we can use the properties of right triangles and trigonometric ratios.
Step 1: Understand the scenario
We have a mountain where the angle of elevation to the summit from the foot of the mountain is 45∘. After ascending 600 meters at an incline of 30∘, the angle of elevation changes to 60∘.
Step 2: Set up the diagram
Let's denote:
- A as the foot of the mountain,
- B as the point after ascending 600 meters,
- C as the summit of the mountain.
Step 3: Use trigonometric ratios
1. From point A (foot of the mountain), the height h of the mountain can be expressed using the tangent of the angle of elevation:
tan(45∘)=hd
Since tan(45∘)=1, we have:
h=d
where d is the horizontal distance from point A to the base of the mountain directly below point C.
2. From point B (after ascending), the height of the mountain can be expressed using the angle of elevation of 60∘:
tan(60∘)=h−600sin(30∘)d−600cos(30∘)
Since tan(60∘)=√3 and sin(30∘)=12 and cos(30∘)=√32, we can substitute these values.
Step 4: Substitute values
1. From point B:
√3=h−600⋅12d−600⋅√32
Simplifying gives:
√3=h−300d−300√3
Step 5: Solve the equations
1. We have two equations:
- h=d
- √3(d−300√3)=h−300
2. Substitute h=d into the second equation:
√3(d−300√3)=d−300
Expanding gives:
√3d−300⋅3=d−300
√3d−d=900−300
(√3−1)d=600
d=600√3−1
Step 6: Calculate height
1. Now, substituting d back to find h:
h=d=600√3−1
2. To rationalize the denominator:
h=600(√3+1)(√3−1)(√3+1)=600(√3+1)3−1=300(√3+1)
Final Answer
The height of the mountain is:
h=300(√3+1) meters
We have a mountain where the angle of elevation to the summit from the foot of the mountain is 45∘. After ascending 600 meters at an incline of 30∘, the angle of elevation changes to 60∘.
Let's denote:
- A as the foot of the mountain,
- B as the point after ascending 600 meters,
- C as the summit of the mountain.
1. From point A (foot of the mountain), the height h of the mountain can be expressed using the tangent of the angle of elevation:
tan(45∘)=hd
Since tan(45∘)=1, we have:
h=d
where d is the horizontal distance from point A to the base of the mountain directly below point C.
tan(60∘)=h−600sin(30∘)d−600cos(30∘)
Since tan(60∘)=√3 and sin(30∘)=12 and cos(30∘)=√32, we can substitute these values.
1. From point B:
√3=h−600⋅12d−600⋅√32
Simplifying gives:
√3=h−300d−300√3
1. We have two equations:
- h=d
- √3(d−300√3)=h−300
√3(d−300√3)=d−300
Expanding gives:
√3d−300⋅3=d−300
√3d−d=900−300
(√3−1)d=600
d=600√3−1
1. Now, substituting d back to find h:
h=d=600√3−1
h=600(√3+1)(√3−1)(√3+1)=600(√3+1)3−1=300(√3+1)
The height of the mountain is:
h=300(√3+1) meters
Topper's Solved these Questions
- HEIGHT AND DISTANCEBOOK - LUCENT PUBLICATIONCHAPTER - HEIGHT AND DISTANCEEXERCISE - EXERCISE-12A
56 Videos
- HEIGHT AND DISTANCEBOOK - LUCENT PUBLICATIONCHAPTER - HEIGHT AND DISTANCEEXERCISE - EXERCISE-12B
14 Videos
- GRAPHICAL SOLUTION OF LINEAR EQUATION BOOK - LUCENT PUBLICATIONCHAPTER - GRAPHICAL SOLUTION OF LINEAR EQUATION EXERCISE - EXERCISE-3B
8 Videos
- INDICES AND SURDS BOOK - LUCENT PUBLICATIONCHAPTER - INDICES AND SURDS EXERCISE - Exercise - 2B
14 Videos
Similar Questions
At the foot of a mountain, the elevation of its summit is 45∘. After ascending 1000 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. find the height of the mountain.
View SolutionAt the foot of a mountain the elevation of its summit is 45∘, after ascending 1000m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘ Find the height of the mountain.
View Solution
Knowledge Check
At the foot of a mountain the elevation of its summit is 45∘. After ascending 2000 meter towards the mountain upon an incline of 30∘, the elevation changes to 60∘. What is the height of the mountain.
A2000(√3−1) meterB1000(√3−1) meterC2000(√3+1) meterD1000(√3+1) meterAt the foot of a mountain, the elevation of its summit is 45∘. After ascending 2 km towards the mountain upon an incline of 30∘, the elevation changes to 60∘. The height of the mountain is
A(√3−1)kmB(√3+1)kmC(√3−2)kmD(√3−2)kmAt the foot of the mountain the elevation of its summit is 45∘, after ascending 100 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. The height of the mountain is
A√3+12mB√3−13 mC√3+12√3 mDnone of these
At the foot of a mountain the elevation of its summit is 450; after ascending 1000 m towards the mountain up a slope of 300 inclination, the elevation is fund to be 600 . Find the height of the mountain.
View SolutionAt the foot of a mountain, the angle of elevation of its summit is 45∘. After ascending 1 km towards the mountain up an incline of 30∘, the elevatioon changes to 60∘ (as shown in the given figure). Find the height of the mountain. [Given: √3=1.73.]
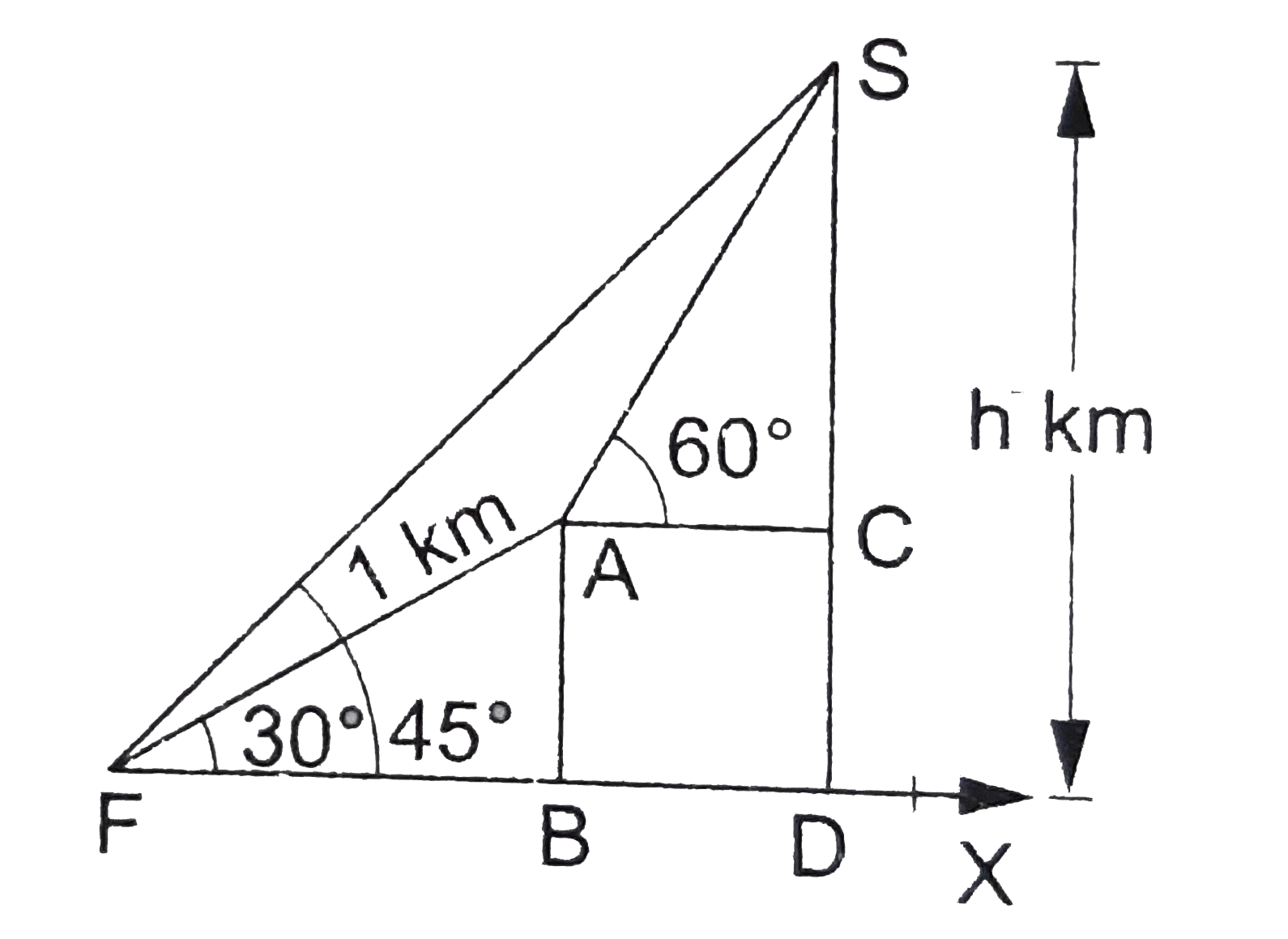
View SolutionAt the foot of a mountain the elevation of it's peak is found to be(π4) ,after ascending 'h' meters toward the mountain up a slope of π6 inclination,the elevation is found to be π3 .Height of the mountain is
View SolutionAt the foot of the mountain, the elevation of its summit is 45∘ , after ascending 1000 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘ . The height of the mountain is
View SolutionFrom a point on the ground, the angle of elevation of a summit is found to be 45∘. After walking 150mt towards the mountain, the angle of elevation of the summit is found to be 60∘. The height of the mountain is:
View Solution
