At the foot of a mountain the elevation of its summit is 450; after ascending 1000 m towards the mountain up a slope of 300 inclination, the elevation is fund to be 600 . Find the height of the mountain.
To find the height of the mountain, we can break down the problem step by step using trigonometric principles.
Step 1: Define the Points
Let:
- Point A be the foot of the mountain.
- Point B be the summit of the mountain.
- Point C be the point after ascending 1000 m towards the mountain.
- Point D be the point directly below B at the same horizontal level as C.
Step 2: Set Up the Angles
At point A, the angle of elevation to point B (the summit) is 45∘. After ascending 1000 m towards the mountain at a slope of 30∘, the angle of elevation to point B from point C is 60∘.
Step 3: Calculate the Height from Point C
From point C, we can use the tangent function to express the height of the mountain in terms of the distance from point C to point D (the vertical height):
tan(60∘)=h−yx
Where:
- h is the height of the mountain (height of point B).
- y is the height of point C above point A.
- x is the horizontal distance from point C to point D.
From the tangent of 60∘:
tan(60∘)=√3⟹√3=h−yx⟹h−y=√3x(1)
Step 4: Calculate the Height from Point A
From point A, we can also express the height of the mountain using the angle of elevation of 45∘:
tan(45∘)=hd
Where d is the horizontal distance from point A to point D:
tan(45∘)=1⟹h=d(2)
Step 5: Relate the Distances
From point C, we know that the horizontal distance d can be expressed in terms of the distance x and the slope of 30∘:
x=1000cos(30∘)=1000⋅√32=500√3
The vertical distance y from point A to point C can be calculated using the sine function:
y=1000sin(30∘)=1000⋅12=500
Step 6: Substitute Values
Now substitute y and x back into equation (1):
h−500=√3(500√3)⟹h−500=1500⟹h=2000
Step 7: Conclusion
Thus, the height of the mountain is:
Height of the mountain=2000 meters=2 km
Let:
- Point A be the foot of the mountain.
- Point B be the summit of the mountain.
- Point C be the point after ascending 1000 m towards the mountain.
- Point D be the point directly below B at the same horizontal level as C.
At point A, the angle of elevation to point B (the summit) is 45∘. After ascending 1000 m towards the mountain at a slope of 30∘, the angle of elevation to point B from point C is 60∘.
From point C, we can use the tangent function to express the height of the mountain in terms of the distance from point C to point D (the vertical height):
- h is the height of the mountain (height of point B).
- y is the height of point C above point A.
- x is the horizontal distance from point C to point D.
tan(60∘)=√3⟹√3=h−yx⟹h−y=√3x(1)
From point A, we can also express the height of the mountain using the angle of elevation of 45∘:
tan(45∘)=1⟹h=d(2)
From point C, we know that the horizontal distance d can be expressed in terms of the distance x and the slope of 30∘:
Now substitute y and x back into equation (1):
Thus, the height of the mountain is:
Topper's Solved these Questions
Similar Questions
At the foot of a mountain the elevation of its summit is 450; after ascending 1000 m towards the mountain up a slope of 300 inclination, the elevation is fund to be 600 . Find the height of the mountain.
View SolutionAt the foot of a mountain the elevation of its summit is 45∘, after ascending 1000m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘ Find the height of the mountain.
View Solution
Knowledge Check
At the foot of the mountain, the elevation of its summit is 45∘ , after ascending 1000 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘ . The height of the mountain is
A√3+12mB√3−12mC√3+12√3Dnone of theseAt the foot of the mountain the elevation of its summit is 45∘, after ascending 100 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. The height of the mountain is
A√3+12mB√3−13 mC√3+12√3 mDnone of theseAt the foot of a mountain the elevation of its summit is 45∘. After ascending 2000 meter towards the mountain upon an incline of 30∘, the elevation changes to 60∘. What is the height of the mountain.
A2000(√3−1) meterB1000(√3−1) meterC2000(√3+1) meterD1000(√3+1) meter
At the foot of a mountain, the elevation of its summit is 45∘. After ascending 1000 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. find the height of the mountain.
View SolutionAt the foot of a mountain the elevation of its summit is 45∘. After ascending 600 meter towards the mountain, upon an incline of 30∘, the elevation changes to 60∘. Find the height of the mountain.
View SolutionAt the foot of a mountain the elevation of it's peak is found to be(π4) ,after ascending 'h' meters toward the mountain up a slope of π6 inclination,the elevation is found to be π3 .Height of the mountain is
View SolutionAt the foot of a mountain, the angle of elevation of its summit is 45∘. After ascending 1 km towards the mountain up an incline of 30∘, the elevatioon changes to 60∘ (as shown in the given figure). Find the height of the mountain. [Given: √3=1.73.]
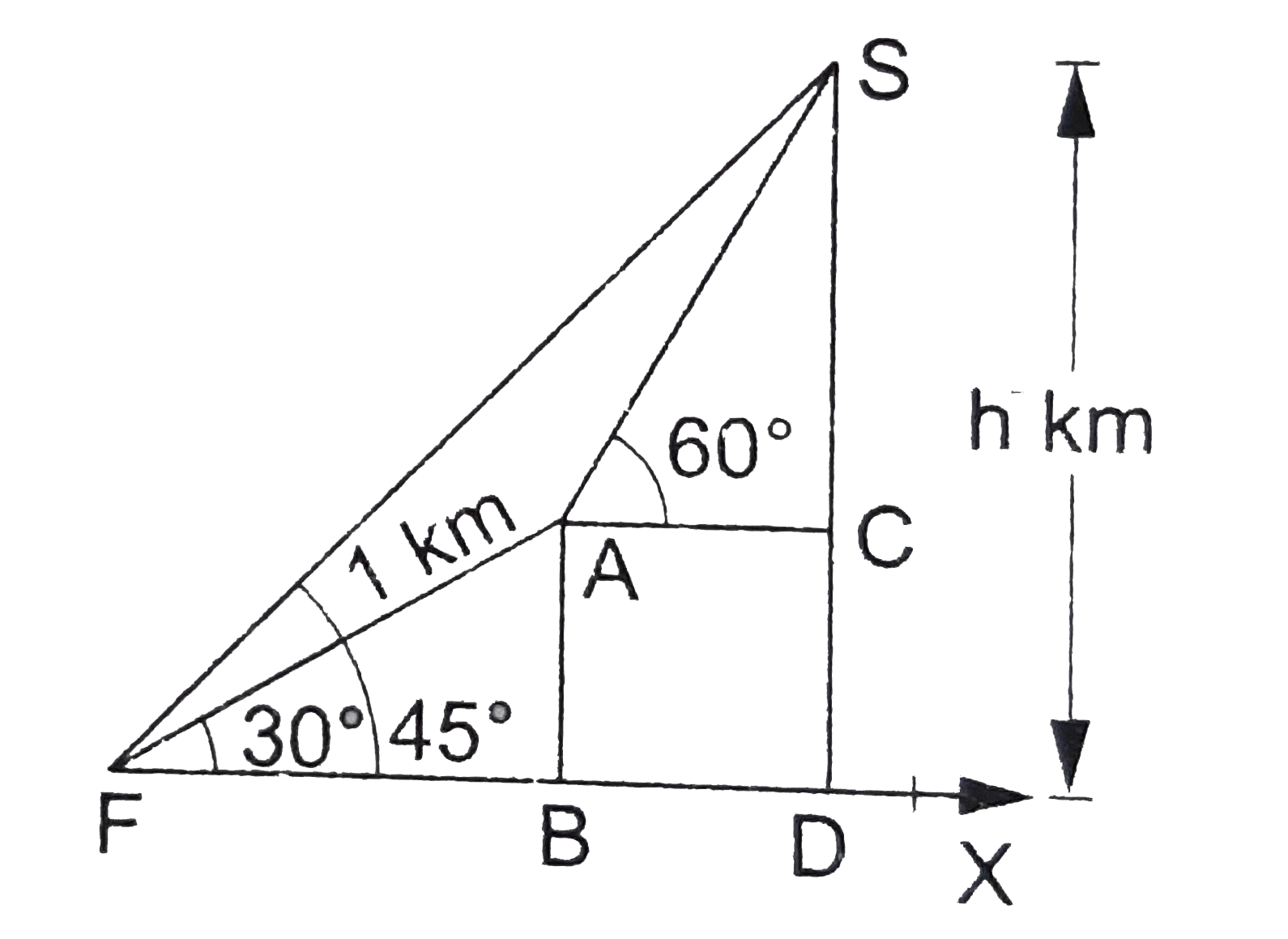
View SolutionAt the foot of a mountain, the elevation of its summit is 45∘. After ascending 2 km towards the mountain upon an incline of 30∘, the elevation changes to 60∘. The height of the mountain is
View Solution
