Define power of a lens. Write its units. Deduce the relation 1f = 1f1 + 1f2 for two thin lenses kept in contact coaxially.
The correct Answer is:0.6 J/T
Similar Questions
Knowledge Check
Power (P) of a lens is given by reciprocal of focal length (f) of the lens. i.e. P=1/f. When f is in metre, P is in dioptre. For a convex lens, power is positive and for a concave lens, power is negative. When a number of thin lenses of powers p1,p2,p3.... are held in contact with one another, the power of the combination is given by algebraic sum of the powers of all the lenses
i.e., P=p1+p2+p3+........
Answer the following questions :
Two thin lenses are in contact and the focal length of the combination is 80cm. If the focal length of one lens is 20cm, the focal length of the other would beA−26.7cmB60cmC80cmD20cmIf two power of a thick lense is P1 and that of a thin lens is P2 then
AP1<P2BP1=P2CP1>P2DP1=P22
(a) Using the ray diagram for a system of two lenses of focal lengths f1andf2 in contact with each other, show that the two lens system can be regarded as equivalent to a single lens of focal length f, where
1f=1f1+1f2
Also write the relation for the equivalent power of the lens combination.
(b) Determine the position of the image formed by the lens combination given in the figure.
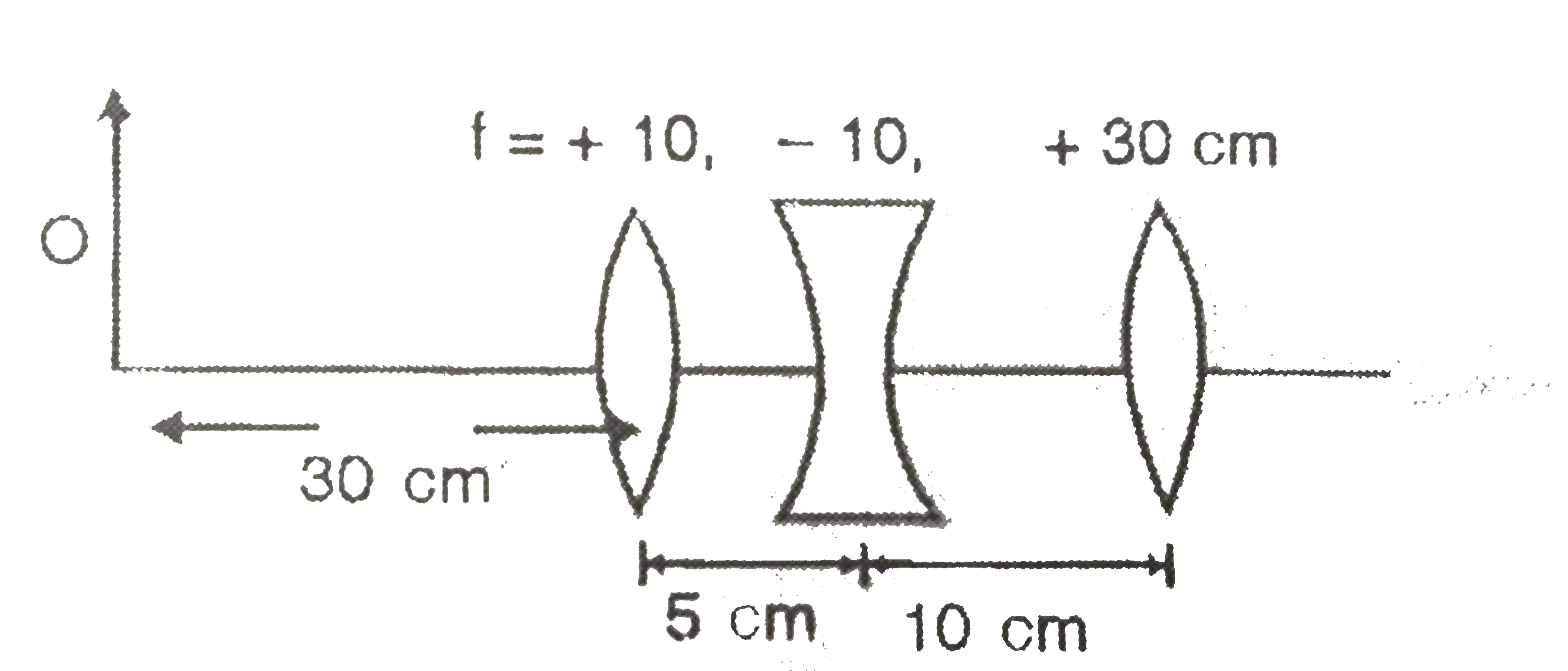
View Solution(a) Using the ray diagram for a system of two lenses of focal lengths f1andf2 in contact with each other, show that the two lens system can be regarded as equivalent to a single lens of focal length f, where
1f=1f1+1f2
Also write the relation for the equivalent power of the lens combination.
(b) Determine the position of the image formed by the lens combination given in the figure.
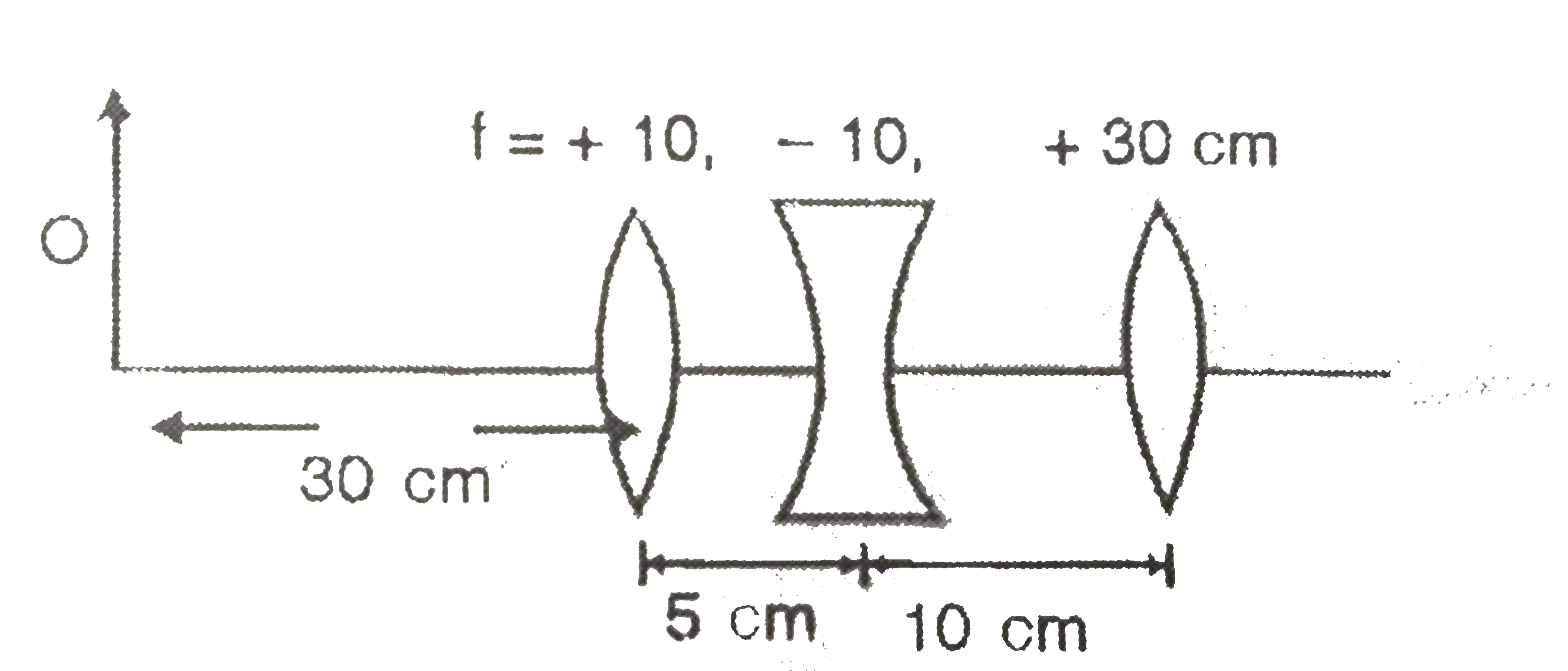
View SolutionThe power of lens is P=1f' where f is focal length of the lens. The dimensions of power of lens is
View SolutionThe power of lens is P=1f' where f is focal length of the lens. The dimensions of power of lens is
View SolutionDerive the relation : 1F=1f1+1f2,where f1 and f2 are focal length of two thin lenses and F is the focal length of the combination in contact.
View SolutionFor two thin lenses kept in contact with each other, show that :
1F=1f1+1f2
where the terms have their usual meaning.
View Solution
