A battery of 10V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω. Determine equivalent resistance of the network and the current through the battery.Solution in Punjabi
Step by step video & image solution for A battery of 10V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1 Omega. Determine equivalent resistance of the network and the current through the battery. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTRICAL MEASUREMENTSBOOK - MODERN PUBLICATIONCHAPTER - ELECTRICAL MEASUREMENTSEXERCISE - EXERCISE
44 Videos
- ELECTRIC POTENTIALBOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC POTENTIALEXERCISE - EXERCISE
38 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
146 Videos
Similar Questions
State and explain Kirchhoff's laws.
View SolutionFind an expression for line integral of electric intensity.
View SolutionExplain the concept of magnetic flux linked with a surface.
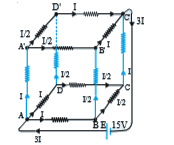
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
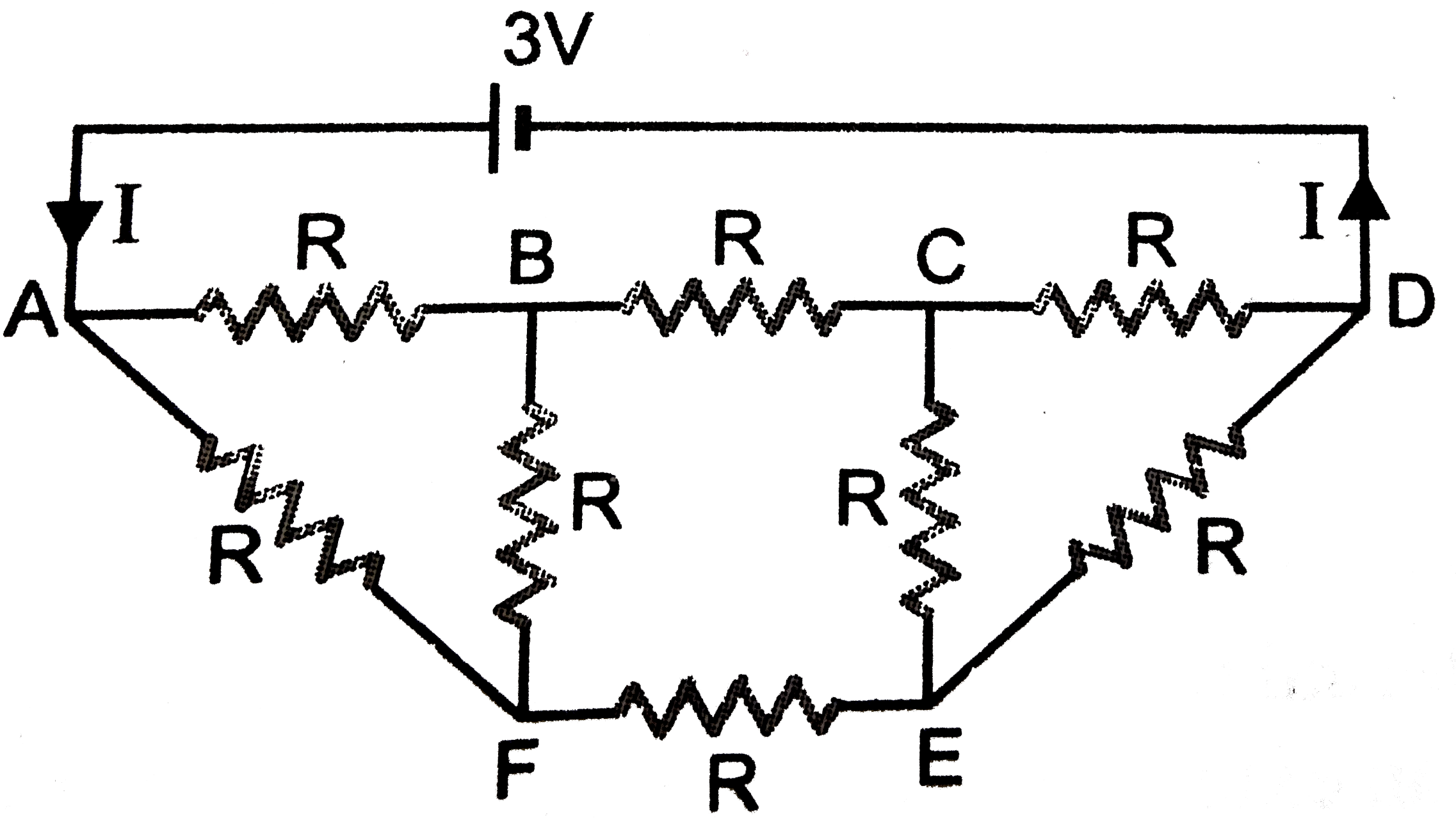
View SolutionShows a network of eight resistors battery of resistance R(=2Ω) connected in a 3V battery of negligible internal resistance. The current I in the circuit is
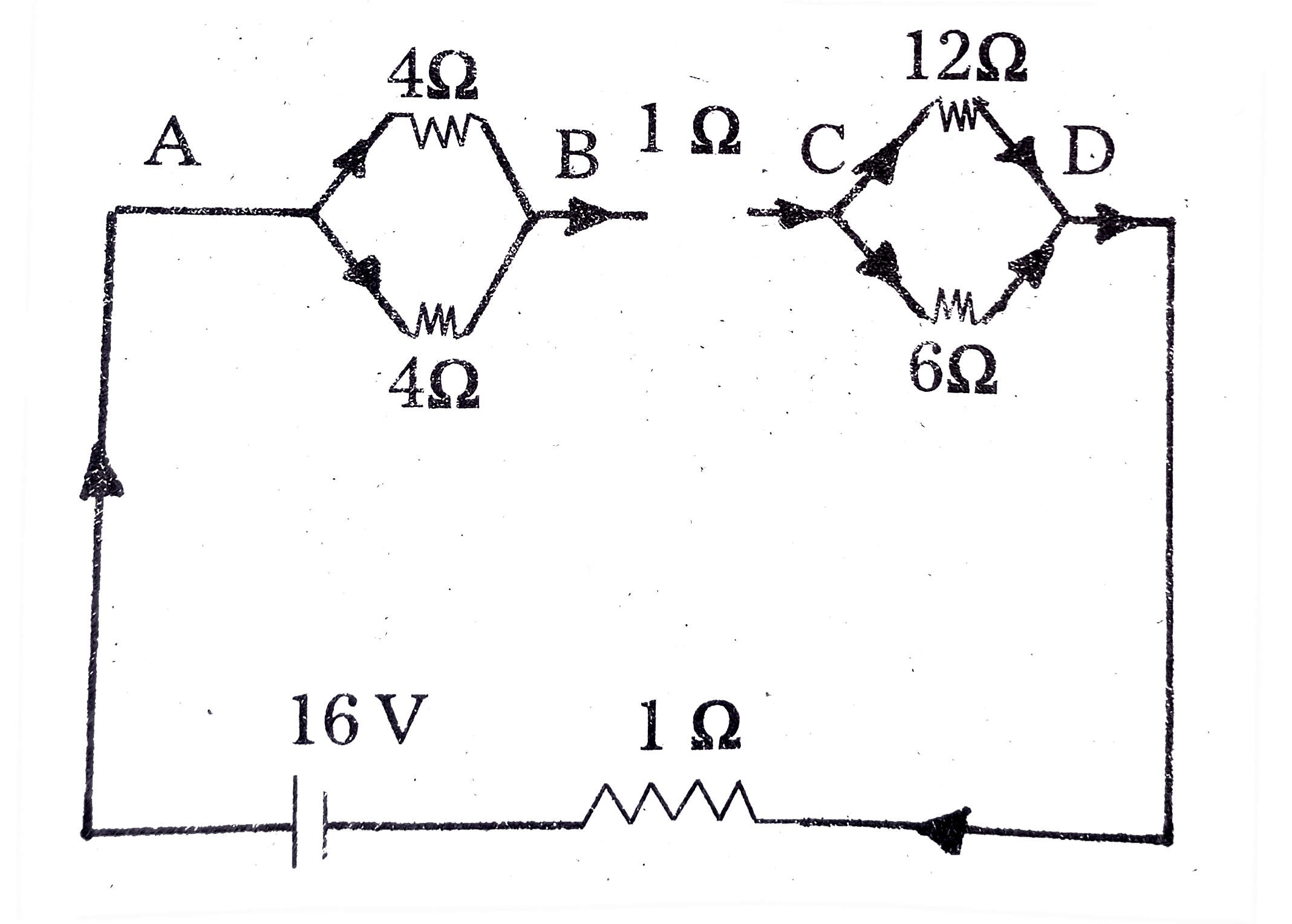
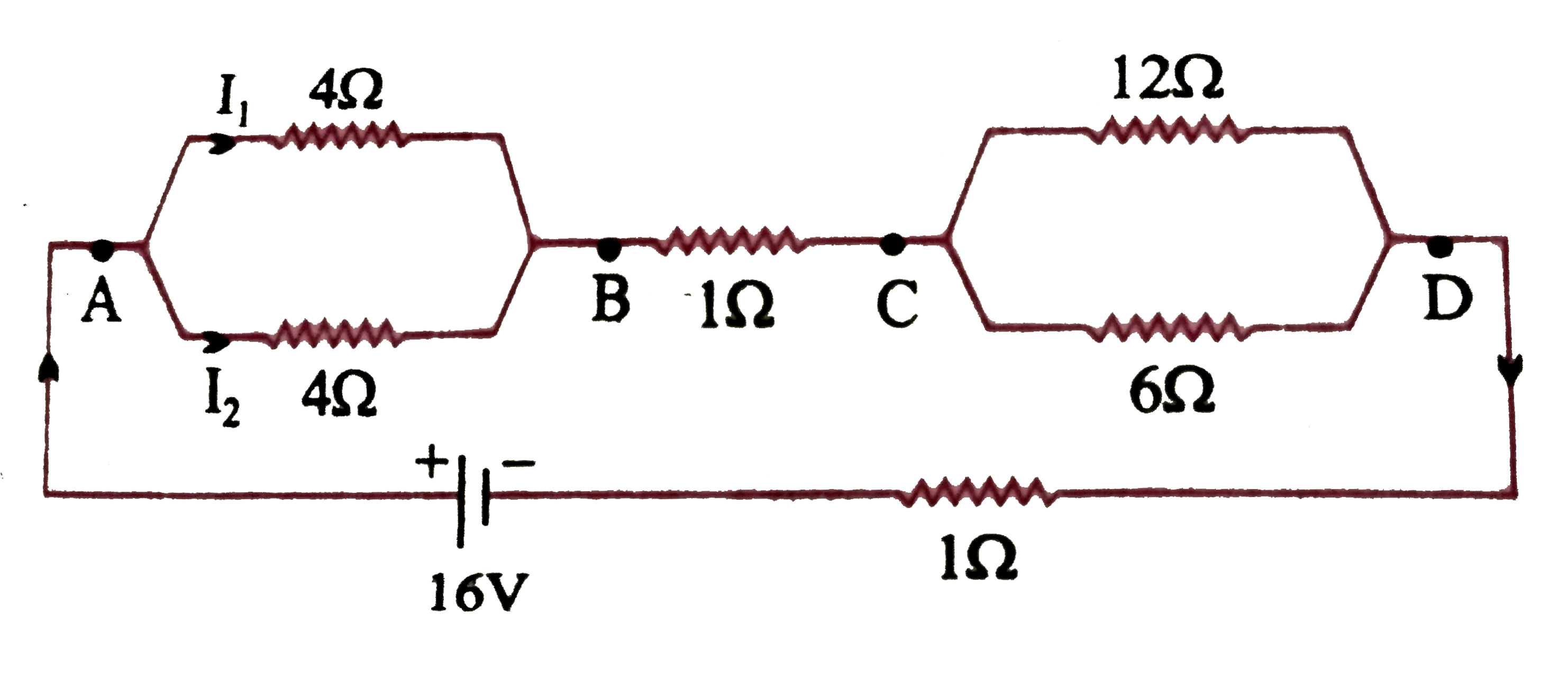
View SolutionA network of resistors is connected to a battery of negligible internal resistance, as shown in figure. Calculate the equivalent resistance between the point A and D, and the value of the current I_(3) .
View SolutionBattery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1 Omega (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
View SolutionA network of resistor is connected to a 16 V battery with internal resistance of 1 Omega , a shown in fig. (a) complete the equivalent resistance of the network.
View SolutionA network of resistor is connected to a 16 V battery with internal resistance of 1Ω, a shown in fig.
Obtain the current in each resistor.
View Solutionनिम्न चित्र के अनुसार 1Ω आंतरिक प्रतिरोध के 16 V कि एक बैटरी से प्रतिरोधों के एक नेटवर्क को जोड़ा गया है ।
नेटवर्क के तुल्य प्रतिरोध कि गणना कीजिए ।
View SolutionTwelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
View Solutionचित्र में दिखाए गए अनुसार आंतरिक 1Ω प्रतिरोध के की एक बैटरी में प्रतिरोधों के 16 V एक नेटवर्क को जोड़ा गया है
नेटवर्क का तुल्य प्रतिरोध परिकलित कीजिये |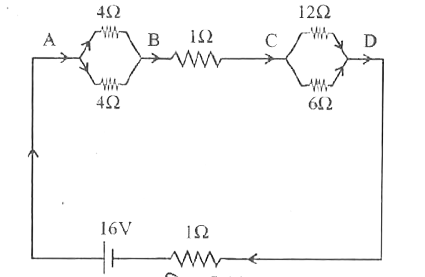
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Omega 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
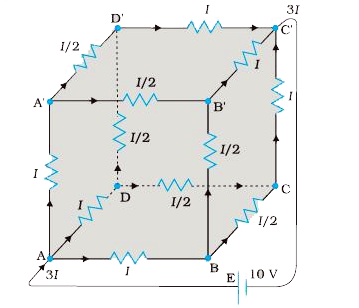
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
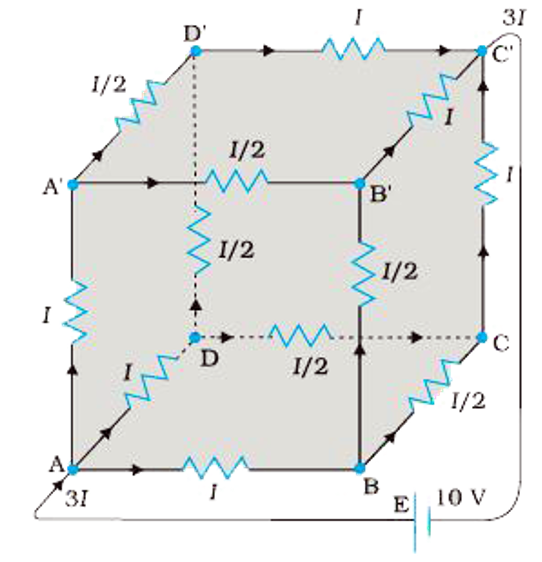
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
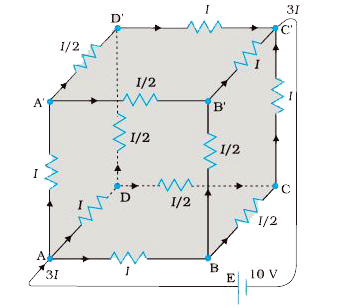
View Solution
