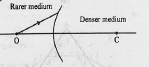
Starting new cartesian sign conventions, derive the relation. −μ1u+μ2v=μ2−μ1R, when refraction occurs from rarer to denser medium at convex spherical refracting surface (μ1<μ2). Where u, v and R are object distance, image distance and radius of curvature of spherical surface respectively.Solution in Punjabi
Step by step video & image solution for Starting new cartesian sign conventions, derive the relation. -frac(mu_1)(u)+frac(mu_2)(v)=frac(mu_2-mu_1)(R), when refraction occurs from rarer to denser medium at convex spherical refracting surface (mu_1 lt mu_2). Where u, v and R are object distance, image distance and radius of curvature of spherical surface respectively. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - MODERN PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - EXERCISE
168 Videos
- REFLECTION OF LIGHTBOOK - MODERN PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISE
57 Videos
- SEMICONDUCTOR DEVICESBOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE
174 Videos
Similar Questions
Explain the phenomenon of refraction at a plane surface separating two transparent media and show that μ=c/v where letters have their usual meanings.
View SolutionState the characteristis of image formed by a plane mirror.
View SolutionExplain the two processes involved in the formation of a p-n junciton diode. Hence defien the term"barrier potential".
View SolutionThe equation of refraction at a spherical surface is μ2v−μ1u=μ2−μ1R
Taking R=∞, show that this equation leads to the equation
RealdepthApparentdepth=μ2μ1 for fraction at a plane surface.
View SolutionFigure shows figure three transparent medi of refractive indices μ1,μ2andμ3. A point object O is placed in the medium μ2. If the entire medium on the right of the spherical surface has refractive index μ1, the image forms at O. If this entire medium has refractive index μ2 the image form at O''. In the situation shown

View SolutionProve that −μ1u+μ2v=μ2−μ1R when refraction occurs from rarer to denser medium at a concave spherical refracting surface.
View SolutionWhen refraction occurs from denser to……….., then (mu_2)/(mu_1) = …………. .
View SolutionA double convex lens, made from a material of refractive index mu_1 , is immersed in a liquid of refractive index mu_2 , where mu_2 gt mu_1 . What change, if any, would occur in the nature of the lens?
View SolutionA Plane convex lens of refractive index mu_1 and focal length f_1 is kept in contact with another plane concave lens of refractive index mu_2 and focal length f_2 If the radius of curvature of their spherical faces is R each and f_1 = 3 f_2 then mu_1 " and " mu_2 are related as:
View SolutionFigure shows three transparent media of refractive indices μ1,μ2andμ3. A point object O is placed in the medium μ2. If the entire medium on the right of the spherical surface has refractive index μ1, the image forms at O'. If this entire medium has refractive index μ3 the image form at O''. In the situation shown

View SolutionBy stating the sign conventions and assumptions used, derive the relation between distance of object, distance of image and radius of curvature of convex spherical surfaces, when refraction takes from optically rarer to optically denser medium.
View SolutionProve the following formula when refraction takes place at a convex spherical refracting surface and source of light lies in the rarer medium and image formed is real μ2v−μ1u=μ2−μ1R Where the terms have their usual meanings.
View SolutionStarting new cartesian sign conventions, derive the relation. -frac(mu_1)(u) + frac(mu_2)(v) = frac(mu_2-mu_1)(R) , when refraction occurs from rarer to denser medium at convex spherical refracting surface (mu_1 lt mu_2) . Where u, v and R are object distance, image distance and radius of curvature of spherical surface respectively.
View SolutionA convex lens made of a material of refractive index μ1 , is kept in a medium of refractive index μ2, Parallel rays of light are incident on the lens. Complete the pathof rays of light emerging from the convex lens if μ1=μ2.
View SolutionDerive the relation:- frac(mu_2)(v) - frac(mu_1)(u) = frac(mu_2 - mu_1) (R) when light undergoes refraction fromoptically rarer to optically denser medium at curved surface.
View SolutionA spherical surface of radius of curvature R, seperates a rarer and a denser medium as shown in the figure.Derive the relation connecting object distance .u., image distance .v., radius of curvature R and the refractive indices n1 and n2 of the two media.
View Solution
