What is the area (∈cm2) of a regular hexagon of side 9 cm is equal to ? (A) 50√3cm2 (B) 300√3cm2 (C) 243√32cm2 (D) 200√3cm2
(a)A
(b)D
(c)B
(d)C
To find the area of a regular hexagon with a side length of 9 cm, we can use the formula for the area of a regular hexagon:
Area=3√32×side2
Step 1: Identify the side length
The side length of the hexagon is given as 9 cm.
Step 2: Substitute the side length into the formula
Substituting the side length into the area formula:
Area=3√32×(9)2
Step 3: Calculate 92
Calculating 92:
92=81
Step 4: Substitute 81 back into the formula
Now substitute 81 back into the formula:
Area=3√32×81
Step 5: Multiply 3 and 81
Now calculate 3×81:
3×81=243
Step 6: Divide by 2
Now divide 243 by 2:
Area=243√32
Final Answer
Thus, the area of the regular hexagon is:
Area=243√32 cm2
The correct option is (C) 243√32 cm2.
---
The side length of the hexagon is given as 9 cm.
Substituting the side length into the area formula:
Calculating 92:
Now substitute 81 back into the formula:
Now calculate 3×81:
Now divide 243 by 2:
Thus, the area of the regular hexagon is:
Similar Questions
Knowledge Check
The area of a regular hexagon of side 2√3 cm is :
A18√3cm2B12√3cm2C36√3cm2D27√3cm2The area of a regular hexagon of side 2√3 cm is :
A18√3cm2B12√3cm2C36√3cm2D27√3cm2The area of a regular hexagon of side 2√3 cm is
A18√3cm2B12√3cm2C36√3cm2D27√3cm2
If the area of a regular hexagon 96√3 is square cm, then its perimeter is:
View SolutionThe area of an equilateral triangle with side 2√3 cm is
View SolutionIn the adjoining figure, the length of BC is
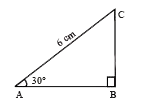
(a)2√3 cm
(b)3√3 cm
(c)4√3 cm
(d)3 cm
View SolutionThe altitude of an equllateral triangle of side 2√3 cm is
View SolutionThe altitude of an equilateral triangle of side 2√3 cm is -----
View Solution
