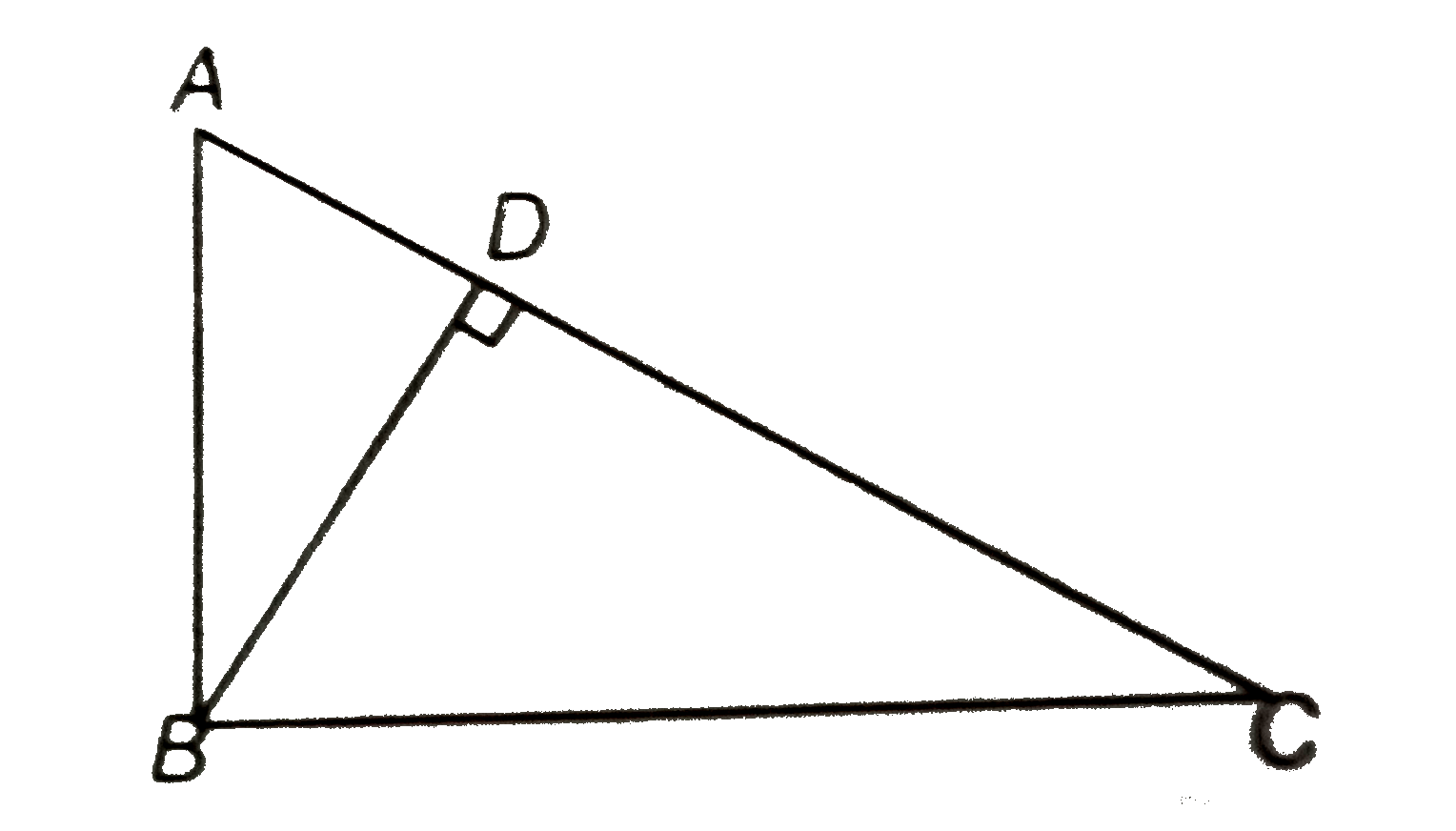
$△ A B C$ is right angled at B. BD is an altitude AD+4 cm and DC = 9 cm. what is the value of BD?
(A) 5 cm (B) 4.5 cm (C) 5.5 cm (D) 6 cm

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to find the length of the altitude $B D$ in triangle $A B C$ which is right-angled at $B$ . We are given that $A D = 4$ cm and $D C = 9$ cm.
1. Identify the lengths:
- $A D = 4$ cm
- $D C = 9$ cm
- Therefore, the total length $A C = A D + D C = 4 + 9 = 13$ cm.
2. Let $B D = x$ :
- We will denote the length of the altitude $B D$ as $x$ .
3. Apply the Pythagorean theorem in triangle $A B D$ :
- In triangle $A B D$ , we have:
$A B^{2} = A D^{2} + B D^{2}$
- Substituting the known values:
$A B^{2} = 4^{2} + x^{2} = 16 + x^{2}$
4. Apply the Pythagorean theorem in triangle $B C D$ :
- In triangle $B C D$ , we have:
$B C^{2} = B D^{2} + D C^{2}$
- Substituting the known values:
$B C^{2} = x^{2} + 9^{2} = x^{2} + 81$
5. Apply the Pythagorean theorem in triangle $A B C$ :
- In triangle $A B C$ , we have:
$A C^{2} = A B^{2} + B C^{2}$
- Substituting the expressions we found:
$13^{2} = (16 + x^{2}) + (x^{2} + 81)$
- Simplifying:
$169 = 16 + x^{2} + x^{2} + 81$
$169 = 2 x^{2} + 97$
6. Rearranging the equation:
- Move 97 to the other side:
$169 - 97 = 2 x^{2}$
$72 = 2 x^{2}$
$x^{2} = \frac{72}{2} = 36$
7. Finding $x$ :
- Taking the square root:
$x = \sqrt{36} = 6$
Thus, the value of $B D$ is $6$ cm.
Final Answer:
The value of $B D$ is $6$ cm, which corresponds to option (D).

Updated on:8/8/2024

$∠ A$ of $Δ A B C$ is a right angle. AD is perpendicular on BC. If BC = 14 cm and BD = 5 cm, then measure of AD is :
A $2 \sqrt{5} c m$ .
B $\sqrt{5} c m$ .
C $3 \sqrt{5} c m$ .
D $3.5 \sqrt{5} c m$ .
$T r i ∠ A B C$ a right triangle has $∠ B = 90^{\circ}$ and AC is hypotenuse D is its circumcentre and AB=3 cms ,BcC=4cms the value of BD is
A3cms
B4cms
C2.5cms
D5.5cms