ABCD is a rectangle. The diagonals AC and BD intersect at O. If AB = 32 cm and AD = 24 cm, then what is OD equal to ?
A. 22 cm
B. 20 cm
C. 18 cm
D. 16 cm
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the properties of the rectangle
We know that in a rectangle, the diagonals bisect each other and all angles are right angles (90 degrees).
Hint: Remember that the diagonals of a rectangle are equal in length and they intersect at the midpoint.
Step 2: Identify the lengths of the sides
Given:
- AB (length) = 32 cm
- AD (width) = 24 cm
Hint: Label the sides of the rectangle clearly to avoid confusion.
Step 3: Use the Pythagorean theorem to find the length of the diagonal BD
In triangle ABD, we can use the Pythagorean theorem:
BD2=AB2+AD2
BD2=322+242
BD2=1024+576
BD2=1600
BD=√1600=40 cm
Hint: The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Step 4: Find the length of OD
Since the diagonals bisect each other, we know that:
OD=BD2
OD=402=20 cm
Hint: Remember that the diagonals of a rectangle split each other into two equal parts.
Final Answer
Thus, the length of OD is 20 cm.
We know that in a rectangle, the diagonals bisect each other and all angles are right angles (90 degrees).
Given:
- AB (length) = 32 cm
- AD (width) = 24 cm
In triangle ABD, we can use the Pythagorean theorem:
BD2=AB2+AD2
BD2=322+242
BD2=1024+576
BD2=1600
BD=√1600=40 cm
Since the diagonals bisect each other, we know that:
OD=BD2
OD=402=20 cm
Thus, the length of OD is 20 cm.
Similar Questions
Knowledge Check
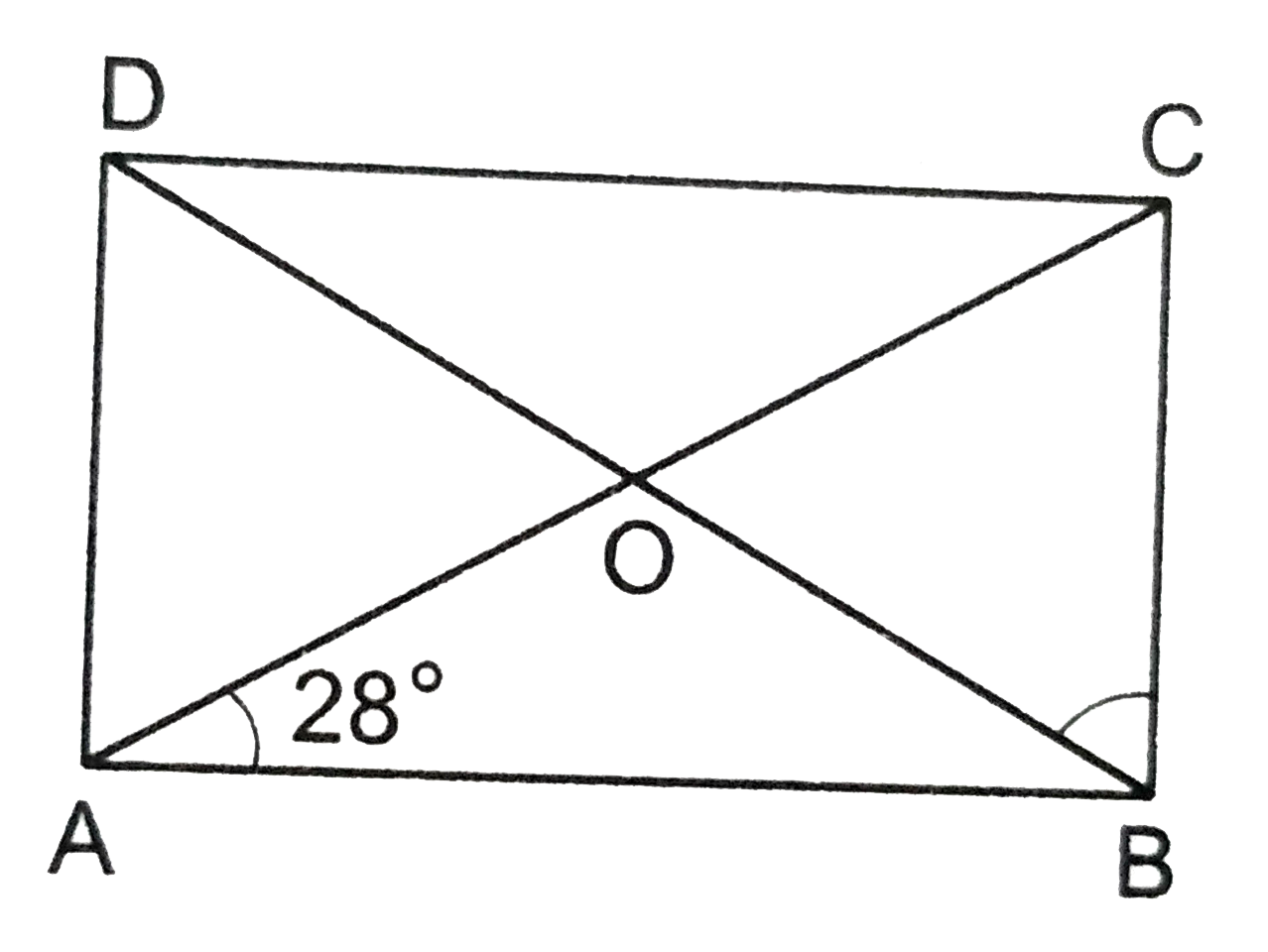
In the given figure, ABCD is a rectangle whose diagonals AC and BD intersect at 0. If ∠OAB=28∘, then ∠OBC is equal to
 A72∘B50∘C62∘D75∘
A72∘B50∘C62∘D75∘In the given figure, ABCD is a ||gm in which diagonals AC and BD intersect at O. If ar(||gm ABCD) is 52cm2 then the ar(△AOB)=?
 A26cm2B18.5cm2C39cm2D13cm2
A26cm2B18.5cm2C39cm2D13cm2In ΔABC,∠B=90∘ and BD⊥AC. If AC = 9 cm and AD = 3 cm, then BD is equal to :
A2√2 cmB3√2 cmC2√3 cmD3√3 cm
In the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB=28∘, find ∠OBC.
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC =12.6 cm and BD = 9.4 cm. Find the measures of OC and OD.
View SolutionIn the adjacent figure , ABCD is a rhombus whose diagonals AC and BD intersect at a point O. If side AB=10 cm and diagonal BD=16 cm , find the length of diagonal AC.
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC = 7.4 cm and BD = 6.2 cm. Find the length of AO and BO.
View Solution□ABCD is a parallelogram. The diagonals AC and BD intersect at point M. The length of seg AC, AB and AD is 24, 22 and 34 respectively. Find the length of seg BD.
View Solution

