Find an expression for an electric field at any position on the equatorial line of an electric dipole .

Text Solution

Verified by Experts

Consider an electric dipole consisting of two point charges $+ q$ and $- q$ separated by a small distance AB =2 l with centre at O and dipole moment p = q (2l) as shown in figure .

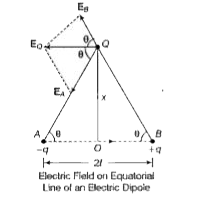
Resultant electric field intensity at the point O is $E_{Q} = E_{A} + E_{B}$
The vector $E_{A}$ and $E_{B}$ are acting at an angle $2 θ$
Here , $E_{A} = \frac{1}{4 π ε_{0}} \cdot \frac{q}{x^{2} + l^{2}}$
$E_{B} = \frac{1}{4 π ε_{0}} \cdot \frac{q}{x^{2} + l^{2}}$
On resolving $E_{A}$ and $E_{B}$ into two rectangular component . The vector $E_{A} sin θ$ and $E_{B} sin θ$ are equal in magnitude and opposite to each other and hence cancel out .
The vector $E_{A} cos θ$ and $E_{B} cos θ$ are acting along the same direction and hence add up .
$∴ E_{Q} = E_{A} cos θ + E_{B} cos θ$
$= 2 E_{A} cos θ (E_{A} = E_{B})$
= $\frac{2}{4 π ε_{0}} \cdot \frac{q}{(x^{2} - l^{2})} \cdot \frac{l}{{(x^{2} + l^{2})}^{1 / 2}} [cos θ = \frac{1}{{(x^{2} + l^{2})}^{1 / 2}}] = \frac{1}{4 π ε_{0}} \cdot \frac{2 q l}{{(x^{2} + l^{2})}^{3 / 2}}$ ... (i)
But $q \times 2 l = | p |$ , the dipole moment
$∴ E_{Q} = \frac{1}{4 π ε_{0}} \cdot \frac{| p |}{{(x^{2} + l^{2})}^{3 / 2}}$
The direction of $E_{Q}$ is along QE || BA and opposite to BA . in vector form , we can rewrite as
$E_{Q} = \frac{- p}{4 π ε_{0} {(x^{2} + l^{2})}^{3 / 2}}$
If the dipole is short , $2 l < < x$
$∴ E_{Q} = \frac{1}{4 π ε_{0}} \cdot \frac{| p |}{x^{3}} ...$ (ii)
Clearly , $E_{Q} \propto \frac{1}{x^{3}}$

Updated on:21/07/2023

The electric potential at a point on the equatorial line of a electric dipole is
Adirectly proportional to the square of the distance
Bindirectly proportional to the square of the distance
Cdirectly proportional to the charge
Dnone of the above
For an electric dipole, the field at a point on the equatorial line and the dipole moment are
Ain the same direction
Bin opposite direction
Cperpendicular to each other
Dnot related