Using Gauss's theorem , prove that electric field at any point inside a charged hollow spherical conductor is zero . Draw a graph showing the variation of electric field with distance from the centre of the hollow conductor .

Text Solution

Verified by Experts

Let $σ$ be the uniform surface charge density of a thin spherical shell of radius R . The Gaussian surface will be a spherical surface centred at the centre of shell as shown in the figure having radius r .

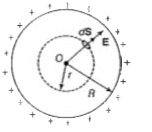
Here , charge inside the Gaussian surface is zero .
i.e, q = 0
$∴ ϕ E \cdot d S = \frac{q}{ε_{0}}$
$\Rightarrow \oint E d S {cos 0}^{\circ} = 0 \Rightarrow E ϕ d S = 0$
$\Rightarrow E (4 π r^{2}) = 0 \Rightarrow E = 0$
The variation of electric field with distance r from the centre of the hollow conductor is shown as below

Updated on:21/07/2023

Electric potential at the center ofa charged hollow spherical conductor is
Azero
Btwice as that on the surface
Chalf of that on the surface
Dsame as that on the surface
Inside a charged hollow spherical conductor. the potential :-
Ais constant
Bvaries directly as the distance from the centre
Cvaries inversely as the distance from the centre
Dvaries inversely as the square of the distance from the centre
Electric field intensity at a point a hollow charged spherical conductor
Ais zero
Bis constant
Cincrease with the distance from the centre of the sphere
Dnone of these