If a quantity y varies as the sum of three quantities of which the first varies as x, the second varies as −x+x2 the third varies as x3−x2 then what is y equal to ?
kx3 where k is a constant
kx+lx2+mx3, where k,l,m are constants
kx2 where k is a constant
kx where k is a constant
To solve the problem, we need to analyze how the quantity y varies with respect to the three given quantities. Let's break down the solution step by step:
Step 1: Identify the quantities
We are given three quantities that contribute to y:
1. The first quantity varies as x.
2. The second quantity varies as −x+x2.
3. The third quantity varies as x3−x2.
Step 2: Write the expression for y
Since y varies as the sum of these three quantities, we can express y as:
y=k1x+k2(−x+x2)+k3(x3−x2)
where k1,k2,k3 are constants of proportionality.
Step 3: Simplify the expression
Now, we will simplify the expression for y:
y=k1x+k2(−x)+k2(x2)+k3(x3)−k3(x2)
Combining like terms:
y=(k1−k2)x+(k2−k3)x2+k3x3
Step 4: Identify the dominant term
In the expression y=(k1−k2)x+(k2−k3)x2+k3x3, the highest power of x is x3. Therefore, as x becomes large, the term k3x3 will dominate the behavior of y.
Step 5: Conclude the relationship
Thus, we can conclude that:
y varies as k3x3
This means that y can be expressed as:
y=kx3
where k is a constant (specifically k=k3).
Final Answer
Thus, the final answer is:
y=kx3
We are given three quantities that contribute to y:
1. The first quantity varies as x.
2. The second quantity varies as −x+x2.
3. The third quantity varies as x3−x2.
Since y varies as the sum of these three quantities, we can express y as:
y=k1x+k2(−x+x2)+k3(x3−x2)
where k1,k2,k3 are constants of proportionality.
Now, we will simplify the expression for y:
y=k1x+k2(−x)+k2(x2)+k3(x3)−k3(x2)
Combining like terms:
y=(k1−k2)x+(k2−k3)x2+k3x3
In the expression y=(k1−k2)x+(k2−k3)x2+k3x3, the highest power of x is x3. Therefore, as x becomes large, the term k3x3 will dominate the behavior of y.
Thus, we can conclude that:
y varies as k3x3
This means that y can be expressed as:
y=kx3
where k is a constant (specifically k=k3).
Thus, the final answer is:
y=kx3
Similar Questions
Knowledge Check
Suppose y varies as the sum of two quantities of which one vasries directly as x and the other inversely as x. If y=6 when x=4 and y=313 when x=3 then the relation between x and y
Ax=y+4By=2x+8xC7=2x−8xDy=2x−4xA quality x varies inversely as the square of y. Given that x=4, when y=3, the value of x when y=6 is
A1B2C3D4If two quantities x and y vary inversely with each other, then which one of the following is true?
AProduct of their corresponding values remains constant.BSummation of their corresponding values remains constant.CDifference of their corresponding values remains constant.DRatio of their corresponding values remains constant
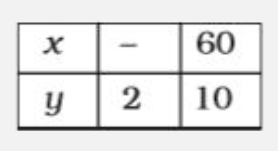
If x varies inversely as y, then
View SolutionIf the velocity "v" of a particle varies as the square of its displacement "x" then the acceleration varies as
View Solution" If the velocity v of a particle varies as the square of its displacement "x" then the acceleration varies as "
View SolutionThe length of the normal to the curve y=acosh(xa) at any point varies as
View SolutionIf a and b vary inversely to each other, then find the values of x, y, z.

View Solution
