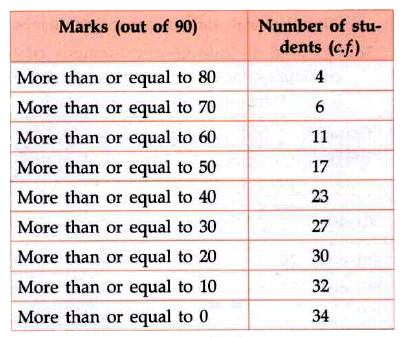
A new frequency distribution is constructed by doubling each frequency of the original distribution keeping the other entries intact. The following measures are computed for both the tables :
1. Arithmetic mean
2. Median
3. Harmonic mean
Which of the following statements with reference to above is correct ?
Corresponding values of 1 and 2 only are equal in both the distributions
Corresponding values of 1 and 3 only are equal in both the distributions
Corresponding values of 2 and 3 only are equal in both the distributions
Corresponding values of 1, 2 and 3 are equal in both the distributions
To solve the problem, we need to analyze how the measures of central tendency (Arithmetic Mean, Median, and Harmonic Mean) change when we double the frequencies in a frequency distribution while keeping the other entries intact.
1. Understanding the Measures:
- Arithmetic Mean (AM): The average of a set of values. For a frequency distribution, it is calculated as:
AM=∑(f⋅x)∑f
where f is the frequency and x is the value.
- Median: The middle value when the data is ordered. In a frequency distribution, it is found by determining the cumulative frequency and identifying the value that corresponds to the median position.
- Harmonic Mean (HM): It is calculated as:
HM=n∑(fx)
where n is the total number of observations.
2. Doubling the Frequencies:
- When we double each frequency, the new frequencies become 2f. The values x remain unchanged.
- The new Arithmetic Mean becomes:
New AM=∑(2f⋅x)∑(2f)=2⋅∑(f⋅x)2⋅∑f=AM
Thus, the Arithmetic Mean remains unchanged.
3. Calculating the Median:
- The median is based on the cumulative frequency. Doubling the frequencies will not change the position of the median since the relative distribution of data does not change. Therefore, the median remains unchanged.
4. Calculating the Harmonic Mean:
- The new Harmonic Mean becomes:
New HM=n∑(2fx)=n2⋅∑(fx)=12⋅HM
Thus, the Harmonic Mean is halved.
5. Conclusion:
- After doubling the frequencies:
- The Arithmetic Mean remains the same.
- The Median remains the same.
- The Harmonic Mean is halved.
- Therefore, the correct statement is that the Arithmetic Mean and Median remain equal, while the Harmonic Mean changes.
Final Answer:
The correct statement is: The Arithmetic Mean and Median remain the same, while the Harmonic Mean is halved.
- Arithmetic Mean (AM): The average of a set of values. For a frequency distribution, it is calculated as:
AM=∑(f⋅x)∑f
where f is the frequency and x is the value.
- Median: The middle value when the data is ordered. In a frequency distribution, it is found by determining the cumulative frequency and identifying the value that corresponds to the median position.
- Harmonic Mean (HM): It is calculated as:
HM=n∑(fx)
where n is the total number of observations.
- When we double each frequency, the new frequencies become 2f. The values x remain unchanged.
- The new Arithmetic Mean becomes:
New AM=∑(2f⋅x)∑(2f)=2⋅∑(f⋅x)2⋅∑f=AM
Thus, the Arithmetic Mean remains unchanged.
- The median is based on the cumulative frequency. Doubling the frequencies will not change the position of the median since the relative distribution of data does not change. Therefore, the median remains unchanged.
- The new Harmonic Mean becomes:
New HM=n∑(2fx)=n2⋅∑(fx)=12⋅HM
Thus, the Harmonic Mean is halved.
- After doubling the frequencies:
- The Arithmetic Mean remains the same.
- The Median remains the same.
- The Harmonic Mean is halved.
- Therefore, the correct statement is that the Arithmetic Mean and Median remain equal, while the Harmonic Mean changes.
The correct statement is: The Arithmetic Mean and Median remain the same, while the Harmonic Mean is halved.
Similar Questions
Knowledge Check
Consider the following measures of central tendency for a set of N number :
1. Arithmetic mean
2. Geometric mean
Which of the above uses/use all the datA ?A1 onlyB2 onlyCBoth 1 and 2DNeither 1 nor 2The mean of the following frequency distribution is 1.46.

Find the missing frequencies.A76,38B36,75C39,66D30,79For a set of discrete numbers, three measures of central tendency are given below
1. Arithmetic mean
2. Median
3. Geometric mean
Which of the above measures may not have a meaningful definition?A1onlyB2onlyC3onlyDAll of them are meaningfully defined
Find the frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46.
View SolutionConsider the following distribution :
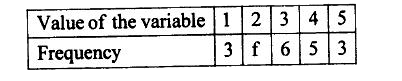
For what value off, is the arithmetic mean of the above distribution 3.1 ?
View SolutionConsider the following statements pertaining to a frequency polygon of a frequency distribution of a continuous variable with seven class intervals of equal width:
1. The original frequency distribution can be reconstructed from the frequency polygon.
2. The frequency polygon touches the x-axis in its extreme right and extreme left.
Which of the above statements is/are correct?
View SolutionFor a set of discrete numbers, three measures of central tendency are given below
1. Arithmetic mean
2. Median
3. Geometric mean
Which of the above measures may not have a meaningful definition?
View SolutionConsider the following statements:
1. The algebraic sum of deviations of a set of values from their arithmetic mean is always zero.
2. Arithmetic mean gt Median gt Mode for a symmetric distribution.
Which of the above statements is/are correct?
View Solution