Consider the following statements pertaining to a frequency polygon of a frequency distribution of a continuous variable with seven class intervals of equal width:
1. The original frequency distribution can be reconstructed from the frequency polygon.
2. The frequency polygon touches the x-axis in its extreme right and extreme left.
Which of the above statements is/are correct?
A) 1 only
B) 2 only
C) Both 1 and 2
D) Neither 1 nor 2
To solve the question, we need to analyze the two statements provided regarding the frequency polygon of a frequency distribution.
1. Understanding Frequency Polygon:
- A frequency polygon is a graphical representation of a frequency distribution. It is created by connecting the midpoints of the top of the bars of a histogram with straight lines.
- It helps visualize the distribution of data and understand its shape.
Hint: Recall that a frequency polygon is formed by connecting the midpoints of the histogram bars.
2. Analyzing Statement 1:
- The first statement claims that the original frequency distribution can be reconstructed from the frequency polygon.
- This is true because the frequency polygon is derived from the histogram, which contains all the necessary information about the frequencies of each class interval. Therefore, if you have the frequency polygon, you can determine the frequencies for each class interval.
Hint: Think about how a histogram relates to the frequency polygon and what information can be extracted from it.
3. Analyzing Statement 2:
- The second statement asserts that the frequency polygon touches the x-axis at its extreme right and extreme left.
- This is also true. In a complete frequency distribution, the polygon will start and end on the x-axis, indicating that there are no frequencies beyond the defined class intervals. Thus, the line will touch the x-axis at both ends.
Hint: Consider the behavior of the frequency polygon at the boundaries of the data range.
4. Conclusion:
- Since both statements are correct, the answer to the question is that both statements are true.
Final Answer:
Both statements are correct.
- A frequency polygon is a graphical representation of a frequency distribution. It is created by connecting the midpoints of the top of the bars of a histogram with straight lines.
- It helps visualize the distribution of data and understand its shape.
- The first statement claims that the original frequency distribution can be reconstructed from the frequency polygon.
- This is true because the frequency polygon is derived from the histogram, which contains all the necessary information about the frequencies of each class interval. Therefore, if you have the frequency polygon, you can determine the frequencies for each class interval.
- The second statement asserts that the frequency polygon touches the x-axis at its extreme right and extreme left.
- This is also true. In a complete frequency distribution, the polygon will start and end on the x-axis, indicating that there are no frequencies beyond the defined class intervals. Thus, the line will touch the x-axis at both ends.
- Since both statements are correct, the answer to the question is that both statements are true.
Both statements are correct.
Similar Questions
Draw a frequency polygon for the following frequency distribution:
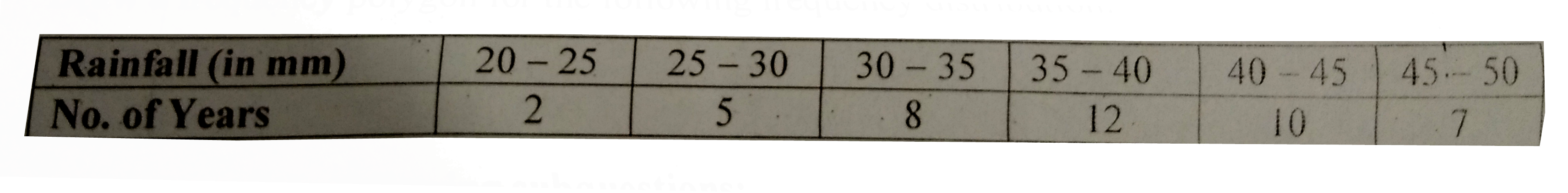
View SolutionDraw frequency polygon for the following frequency distribution.

View SolutionDraw a frequency polygon for the following frequency distribution.

View SolutionDraw the frequency polygon for the following frequency distribution:

View SolutionDraw the frequency polygon for the following distribution :

View SolutionDraw a frequency polygon for the following grouped frequency distribution table :

View SolutionDraw histogram and frequency polygon for the following distribution :

View Solution____ is a graphical presentation of a frequency distribution of a continuous series . (Histogram / Polygon)
View SolutionDraw the frequency polygon representing the following frequency distribution

View SolutionThe following table shows the distribution of weights of seeds. Draw a frequency polygon.
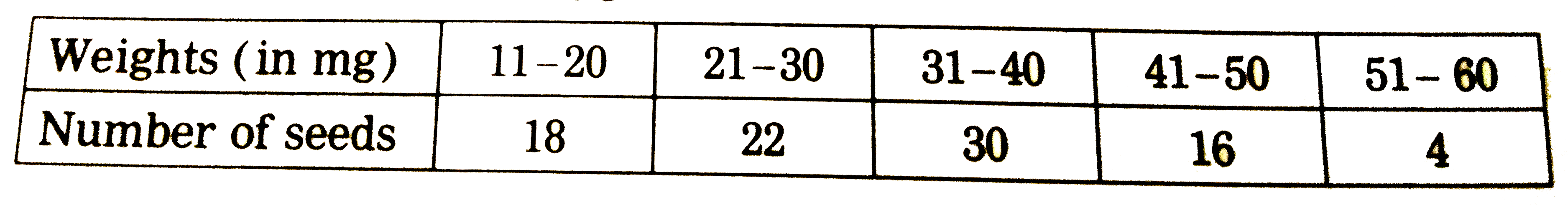
View Solution
