Let ABCD be a quadrilateral. Let the diagonals AC and BD meet at O. Let the perpendicular drawn from A to CD meet CD at E. Further, AO:OC=BO:OD, AB = 30 cm, CD = 40 cm and the area of the quadrilateral ABCD is 1050 cm2.
What is the area of the triangle ADC equal to?
300 cm2
450 cm2
600 cm2
None of the above
To find the area of triangle ADC in the quadrilateral ABCD, we can follow these steps:
1. Understanding the Given Information:
- We have a quadrilateral ABCD with diagonals AC and BD intersecting at point O.
- A perpendicular from point A to line CD meets CD at point E.
- The ratios AO:OC=BO:OD indicate that the diagonals are divided proportionally.
- We know the lengths: AB=30cm, CD=40cm, and the area of quadrilateral ABCD is 1050cm2.
2. Identifying the Shape:
- Since AB∥CD (as established by the alternate angles), ABCD is a trapezium.
3. Using the Area of the Trapezium:
- The area of a trapezium can be calculated using the formula:
Area=12×(AB+CD)×h
where h is the height (distance between the parallel sides).
4. Setting Up the Equation:
- Plugging in the known values:
1050=12×(30+40)×AE
- Simplifying this:
1050=12×70×AE
1050=35×AE
5. Solving for Height (AE):
- Rearranging to find AE:
AE=105035=30cm
6. Finding the Area of Triangle ADC:
- The area of triangle ADC can be calculated using the formula:
Area of △ADC=12×CD×AE
- Substituting the values:
Area of △ADC=12×40×30
- Calculating this:
=12×1200=600cm2
Final Answer:
The area of triangle ADC is 600cm2.
---
- We have a quadrilateral ABCD with diagonals AC and BD intersecting at point O.
- A perpendicular from point A to line CD meets CD at point E.
- The ratios AO:OC=BO:OD indicate that the diagonals are divided proportionally.
- We know the lengths: AB=30cm, CD=40cm, and the area of quadrilateral ABCD is 1050cm2.
- Since AB∥CD (as established by the alternate angles), ABCD is a trapezium.
- The area of a trapezium can be calculated using the formula:
Area=12×(AB+CD)×h
where h is the height (distance between the parallel sides).
- Plugging in the known values:
1050=12×(30+40)×AE
- Simplifying this:
1050=12×70×AE
1050=35×AE
- Rearranging to find AE:
AE=105035=30cm
- The area of triangle ADC can be calculated using the formula:
Area of △ADC=12×CD×AE
- Substituting the values:
Area of △ADC=12×40×30
- Calculating this:
=12×1200=600cm2
The area of triangle ADC is 600cm2.
Similar Questions
Let ABCD be a quadrilateral. Let the diagonals AC and BD meet at O. Let the perpendicular drawn from A to CD meet CD at E. Further, AO:OC=BO:OD, AB = 30 cm, CD = 40 cm and the area of the quadrilateral ABCD is 1050 cm2.
What is BE equal to?View SolutionLet ABCD be a quadrilateral. Let the diagonals AC and BD meet at O. Let the perpendicular drawn from A to CD meet CD at E. Further, AO:OC=BO:OD, AB = 30 cm, CD = 40 cm and the area of the quadrilateral ABCD is 1050 cm2.
What is ∠AEB equal to?View Solution
Knowledge Check
- Question 1 - Select One
ABCD is a rectangle of perimeter 48 cm with AB = 6 cm and CD = DE .What is the area of the triangle ACE ?
 A18cm2B24cm2C30cm2D36cm2
A18cm2B24cm2C30cm2D36cm2 - Question 2 - Select One
ABCD is a quadrilateral in which BD = 40 cm. The lengths of the perpendiculars drawn from the opposite vertices on BD are 16 cm and 12 cm. The area of the quadrilateral (in cm2) is
A560B530C800D500 - Question 3 - Select One
ABCD is a quadrilateral in which BD = 40 cm. The lengths of the perpendiculars drawn from the opposite vertices on BD are 16 cm and 12 cm . The area of the quadrilateral (in cm ) is
A600B500C560D580
In a quadrilateral ABCD it is given tghat AB∣∣CD nad the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionIn a quadrilateral ABCD, AB= AD and CB = CD, prove that AC is perpendicular bisector of BD.
View SolutionIn a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.
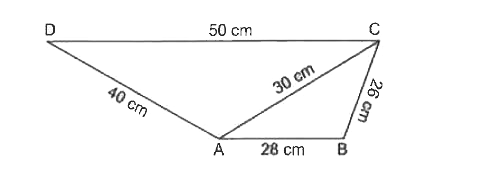 View Solution
View SolutionIn a quadrilateral ABCD, if AB = 10 cm, CD = 6 cm and ∠A+∠D=180∘, what type of quadrilateral is ABCD ?
View SolutionABCD is a quadrilateral in which BD = 40 cm . The lenghtsof the perpendiculars drawn from the opposite vertices on BD are 16 cm and 12 cm . The area of the quadrilateral in (in cm2 ) is
View Solution

