Let ABCD be a quadrilateral. Let the diagonals AC and BD meet at O. Let the perpendicular drawn from A to CD meet CD at E. Further, AO:OC=BO:OD, AB = 30 cm, CD = 40 cm and the area of the quadrilateral ABCD is 1050 cm2.
What is ∠AEB equal to?
30∘
45∘
60∘
None of the above
To solve the problem step by step, we will use the given information about the quadrilateral ABCD, the properties of similar triangles, and the area of a trapezium.
Step 1: Understand the Given Information
We have a quadrilateral ABCD with:
- Diagonals AC and BD intersecting at point O.
- A perpendicular AE drawn from A to line CD, meeting CD at point E.
- Ratios: AO:OC=BO:OD
- Lengths: AB=30cm, CD=40cm
- Area of quadrilateral ABCD = 1050cm2
Step 2: Identify the Type of Quadrilateral
Given that AO:OC=BO:OD and the angles formed at O are vertically opposite, we can conclude that triangles AOB and COD are similar by the Side-Angle-Side (SAS) similarity criterion.
Step 3: Establish Parallel Lines
From the similarity of triangles AOB and COD, we can deduce that:
- ∠AOB=∠COD
- ∠ABE=∠ODC
Since the angles are equal, we can conclude that lines AB and CD are parallel. Therefore, ABCD is a trapezium.
Step 4: Use the Area Formula for Trapezium
The area of a trapezium is given by the formula:
Area=12×(Base1+Base2)×Height
Here, the bases are AB and CD, and the height is AE. Plugging in the values:
1050=12×(30+40)×h
1050=12×70×h
1050=35h
h=105035=30cm
Thus, AE=30cm.
Step 5: Analyze Triangle ABE
In triangle ABE:
- AB=30cm
- AE=30cm
- ∠AEB=90∘ (since AE is perpendicular to CD)
Step 6: Determine Angles in Triangle ABE
Since triangle ABE is isosceles (AB = AE), we can conclude:
∠ABE=∠BEA
Let ∠ABE=∠BEA=x. Then:
x+x+90=180
2x=90
x=45∘
Conclusion
Thus, the measure of ∠AEB is 90∘ and the angles ∠ABE and ∠BEA are both 45∘.
Final Answer
∠AEB=90∘
We have a quadrilateral ABCD with:
- Diagonals AC and BD intersecting at point O.
- A perpendicular AE drawn from A to line CD, meeting CD at point E.
- Ratios: AO:OC=BO:OD
- Lengths: AB=30cm, CD=40cm
- Area of quadrilateral ABCD = 1050cm2
Given that AO:OC=BO:OD and the angles formed at O are vertically opposite, we can conclude that triangles AOB and COD are similar by the Side-Angle-Side (SAS) similarity criterion.
From the similarity of triangles AOB and COD, we can deduce that:
- ∠AOB=∠COD
- ∠ABE=∠ODC
The area of a trapezium is given by the formula:
Area=12×(Base1+Base2)×Height
Here, the bases are AB and CD, and the height is AE. Plugging in the values:
1050=12×(30+40)×h
1050=12×70×h
1050=35h
h=105035=30cm
Thus, AE=30cm.
In triangle ABE:
- AB=30cm
- AE=30cm
- ∠AEB=90∘ (since AE is perpendicular to CD)
Since triangle ABE is isosceles (AB = AE), we can conclude:
∠ABE=∠BEA
Let ∠ABE=∠BEA=x. Then:
x+x+90=180
2x=90
x=45∘
Thus, the measure of ∠AEB is 90∘ and the angles ∠ABE and ∠BEA are both 45∘.
∠AEB=90∘
Similar Questions
Let ABCD be a quadrilateral. Let the diagonals AC and BD meet at O. Let the perpendicular drawn from A to CD meet CD at E. Further, AO:OC=BO:OD, AB = 30 cm, CD = 40 cm and the area of the quadrilateral ABCD is 1050 cm2.
What is BE equal to?
View SolutionLet ABCD be a quadrilateral. Let the diagonals AC and BD meet at O. Let the perpendicular drawn from A to CD meet CD at E. Further, AO:OC=BO:OD, AB = 30 cm, CD = 40 cm and the area of the quadrilateral ABCD is 1050 cm2.
What is the area of the triangle ADC equal to?
View Solution
Knowledge Check
ABCD is a quadrilateral in which BD = 40 cm. The lengths of the perpendiculars drawn from the opposite vertices on BD are 16 cm and 12 cm. The area of the quadrilateral (in cm2) is
A560B530C800D500ABCD is a quadrilateral in which BD = 40 cm. The lengths of the perpendiculars drawn from the opposite vertices on BD are 16 cm and 12 cm . The area of the quadrilateral (in cm ) is
A600B500C560D580ABCD is a quadrilateral in which BD = 40 cm . The lenghtsof the perpendiculars drawn from the opposite vertices on BD are 16 cm and 12 cm . The area of the quadrilateral in (in cm2 ) is
A560B530C800D500
In a quadrilateral ABCD it is given tghat AB∣∣CD nad the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionIn a quadrilateral ABCD, AB= AD and CB = CD, prove that AC is perpendicular bisector of BD.
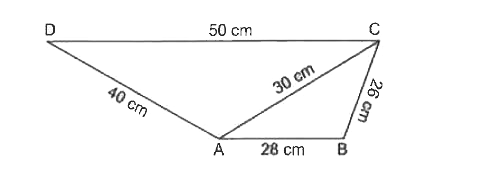
View SolutionIn a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.
View SolutionIn a quadrilateral ABCD, if AB = 10 cm, CD = 6 cm and ∠A+∠D=180∘, what type of quadrilateral is ABCD ?
View SolutionABCD is a rectangle. The diagonals AC and BD intersect at O. If AB = 32 cm and AD = 24 cm, then what is OD equal to ?
View Solution
