In a trapezium ABCD, AB is parallel to DC. The diagonals AC and BD intersect at P. If AP:PC=4:(4x−4) and BP:PD=(2x−1):(2x+4), then what is the value of x ?
A.4
B.3
C.32
D.2
To solve the problem, we need to find the value of x given the ratios of segments formed by the intersection of diagonals in trapezium ABCD.
Step 1: Set up the ratios
We are given:
- AP:PC=4:(4x−4)
- BP:PD=(2x−1):(2x+4)
Step 2: Express the ratios in terms of a common variable
Let:
- AP=4k
- PC=(4x−4)k
From the first ratio:
APPC=4k(4x−4)k=44x−4
Similarly, let:
- BP=(2x−1)m
- PD=(2x+4)m
From the second ratio:
BPPD=(2x−1)m(2x+4)m=2x−12x+4
Step 3: Use the property of similar triangles
Since AB∥DC, triangles APB and CPD are similar. Therefore, we can set up the proportion:
APPC=BPPD
Substituting the ratios we have:
44x−4=2x−12x+4
Step 4: Cross-multiply to solve for x
Cross-multiplying gives:
4(2x+4)=(4x−4)(2x−1)
Expanding both sides:
8x+16=(8x2−4x−8x+4)
8x+16=8x2−12x+4
Step 5: Rearranging the equation
Rearranging gives:
0=8x2−20x−12
Step 6: Simplifying the quadratic equation
Dividing the entire equation by 4:
0=2x2−5x−3
Step 7: Factoring the quadratic
Factoring gives:
(2x+1)(x−3)=0
Step 8: Solving for x
Setting each factor to zero gives:
1. 2x+1=0 → x=−12 (not valid since lengths cannot be negative)
2. x−3=0 → x=3
Conclusion
The value of x is 3.
We are given:
- AP:PC=4:(4x−4)
- BP:PD=(2x−1):(2x+4)
Let:
- AP=4k
- PC=(4x−4)k
APPC=4k(4x−4)k=44x−4
- BP=(2x−1)m
- PD=(2x+4)m
BPPD=(2x−1)m(2x+4)m=2x−12x+4
Since AB∥DC, triangles APB and CPD are similar. Therefore, we can set up the proportion:
APPC=BPPD
44x−4=2x−12x+4
Cross-multiplying gives:
4(2x+4)=(4x−4)(2x−1)
8x+16=(8x2−4x−8x+4)
8x+16=8x2−12x+4
Rearranging gives:
0=8x2−20x−12
Dividing the entire equation by 4:
0=2x2−5x−3
Factoring gives:
(2x+1)(x−3)=0
Setting each factor to zero gives:
1. 2x+1=0 → x=−12 (not valid since lengths cannot be negative)
2. x−3=0 → x=3
The value of x is 3.
Similar Questions
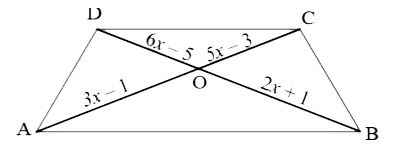
ABCD is a trapezium in which AB parallel to DC and its diagonals intersect at P. If AP = (3x - 1) cm, PC = (5x - 3) cm, BP = (2x + 1) cm and PD = (6x - 5) cm, then the length of DB is:
ABCD एक समलम्ब है जिसमें AB, DC के समानांतर है तथा इसके विकर्ण P पर एक दूसरे को काठते हैं | यदि AP = (3x - 1) सेमी, PC = (5x - 3) सेमी, BP = (2x + 1) सेमी तथा PD = (6x - 5) सेमी है, तो DB की लंबाई क्या होगी ?
View SolutionIn trapezium ABCD side AB∣∣ side DC, diagonals AC and BD intersect In point O. If AB=20,DC=6,OB=15 thn find OD.
View Solution
Knowledge Check
If 4(4x5)>2x−1>4x−3 then the value of x is
A2B3C−2D0If (x4+1x4)=198andx>0 then what is the value of (x2−1x2)
A14B2√7C10√2D10If (x4+1x4)=198andx>0 then what is the value of (x2−1x2)
A14B2√7C10√2D10
In the given fig., AB || DC and diagonals AC and BD intersects at O. If OA =3x-1 and OB =2x + 1, OC = 5x-3 and OD =6x-5, find the value of x.
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC = 7.4 cm and BD = 6.2 cm. Find the length of AO and BO.
View SolutionIf x=1+√2, then what is the value of x4−4x3+4x2 ?
View SolutionABCD is a trapezium in which AB parallel to DC and its diagonals intersect at P. If AP = (3x - 1) cm, PC = (5x - 3) cm, BP = (2x + 1) cm and PD = (6x - 5) cm, then the length of DB is:
ABCD एक समलम्ब है जिसमें AB, DC के समानांतर है तथा इसके विकर्ण P पर एक दूसरे को काठते हैं | यदि AP = (3x - 1) सेमी, PC = (5x - 3) सेमी, BP = (2x + 1) सेमी तथा PD = (6x - 5) सेमी है, तो DB की लंबाई क्या होगी ?
View Solutionif 4x−4x−1=24 then the value of (2x)x equals:
View Solution
