If x varies as mth power of y, y varies as nth power of z and x varies as pth power of z then which one of the following is true?
p=m+n
p=m−n
p=mn
None of these
The correct Answer is:C
To solve the problem step by step, we will analyze the relationships given in the question:
1. Understanding the Variations:
- We know that x varies as the mth power of y. This can be expressed mathematically as:
x=k1ym
where k1 is a constant of variation.
2. Expressing y in terms of x:
- Rearranging the equation gives us:
y=xk1/m1
3. Next, we know that y varies as the nth power of z:
- This can be expressed as:
y=k2zn
where k2 is another constant of variation.
4. Expressing z in terms of y:
- Rearranging this equation gives us:
z=yk1/n2
5. Now substituting y from step 2 into this equation:
- Substituting y=k1zm into z=yk1/n2 gives:
z=k1zmk1/n2
6. Now we know that x varies as the pth power of z:
- This can be expressed as:
x=k3zp
where k3 is another constant of variation.
7. Expressing z in terms of x:
- Rearranging gives us:
z=xk1/p3
8. Substituting z back into the equation for y:
- We can express y in terms of z and then substitute it back into the equation for x:
y=k2⎛⎝xk1/p3⎞⎠n
9. Equating the two expressions for y:
- From the two expressions for y:
xk1/m1=k2⎛⎝xk1/p3⎞⎠n
10. Simplifying the expressions:
- This leads to:
x1−n=k2k−n/p3k1/m1
11. Final Relationship:
- After simplifying, we find that:
p=mn
Thus, the correct relationship is:
p=mn
- We know that x varies as the mth power of y. This can be expressed mathematically as:
x=k1ym
where k1 is a constant of variation.
- Rearranging the equation gives us:
y=xk1/m1
- This can be expressed as:
y=k2zn
where k2 is another constant of variation.
- Rearranging this equation gives us:
z=yk1/n2
- Substituting y=k1zm into z=yk1/n2 gives:
z=k1zmk1/n2
- This can be expressed as:
x=k3zp
where k3 is another constant of variation.
- Rearranging gives us:
z=xk1/p3
- We can express y in terms of z and then substitute it back into the equation for x:
y=k2⎛⎝xk1/p3⎞⎠n
- From the two expressions for y:
xk1/m1=k2⎛⎝xk1/p3⎞⎠n
- This leads to:
x1−n=k2k−n/p3k1/m1
- After simplifying, we find that:
p=mn
p=mn
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - ALGEBRAIC IDENTITIES EXERCISE - Exercise - 1B28videos
ALGEBRAIC IDENTITIES
- BOOK - LUCENT PUBLICATIONCHAPTER - ALGEBRAIC IDENTITIES EXERCISE - Exercise - 1B28videos
ALGEBRAIC IDENTITIES
- BOOK - LUCENT PUBLICATIONCHAPTER - ADVANCED TRIGONOMETRIC IDENTITIESEXERCISE - EXERCISE 13A49videos
ADVANCED TRIGONOMETRIC IDENTITIES
- BOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B8videos
CENTRE OF TRIANGLE
Similar Questions
Knowledge Check
- Question 1 - Select One
If two quantities x and y vary inversely with each other, then which one of the following is true?
AProduct of their corresponding values remains constant.BSummation of their corresponding values remains constant.CDifference of their corresponding values remains constant.DRatio of their corresponding values remains constant - Question 2 - Select One
The 5th , 8th and 11th terms of a G.P. are a,b,c respectively , then which one of the following is true ?
A2b=acBb2=acCa+b+c=0Dnone of these - Question 3 - Select One
The 5th , 8th and 11th terms of a G.P. are a,b,c respectively , then which one of the following is true ?
Aa)2b=acBb)b2=acCc)a+b+c=0Dd)none of these
If x varies inversely as y, then
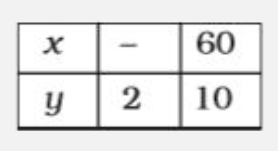 View Solution
View SolutionIf the pth,qth and rth terms of a GP. Are again in G.P., then which one of the following is correct?
View SolutionIf ∣∣ ∣ ∣∣yxy+zzyx+yxzz+x∣∣ ∣ ∣∣=0, then which one of the following is correct ?
View SolutionThe mth term of an A.P. is n and nth term is m its
pth term isView SolutionThe wavelength associated with a moving particle depends upon pth power of its mass m, qth power of its velocity v and power of plank's constant h Then the corrent set of valume of p,q and r is
View Solution

