Let PAB be a secant to a circle intersecting at points A and B, and PC is a tangent. Which one of the following is correct?
Area of the rectangle with PA,PB as adjacent sides is equal to are of square whose side is PC
Area of the rectangle with PA,PC as adjacent sides is equal to area of square whose each side is PB
Area of rectangle with PC, PB as adjacent sides is equal to area of square whose each side is PA
Perimeter of the rectangle with PA, PB as adjacent side is equal to perimeter of the square whose each side is PC.
The correct Answer is:A
Step by step video, text & image solution for Let PAB be a secant to a circle intersecting at points A and B, and PC is a tangent. Which one of the following is correct? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B27videos
CIRCLE AND ITS TANGENT LINES
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B27videos
CIRCLE AND ITS TANGENT LINES
- BOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B8videos
CENTRE OF TRIANGLE
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B8videos
CONGRUENCE AND SIMILAR TRIANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
Tangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
A133B4C154D165
Let PAB be a secant to a circle intersecting the circle at A and B. Let PT be the tangent segment. If PA = 9 cm and PT =12 cm, then what is AB equal to?
View SolutionBisectors of two adjacent angles A and B of a quadrilateral ABCD intersect each other at a point P. Which one of the following is correct?
View SolutionTangent Secant Theorem
Point E is in the exterior of a circle. A secant through E intersects the circle at points A and B, and a tangent through E touches the circle at point T, then EA×EB=ET2.
Given : (1) A circle with centre O
(2) Tangent ET touches the circle at pointT
(3) Secant EAB intersects the circle at points A and B .
To prove : EA×EB=ET2
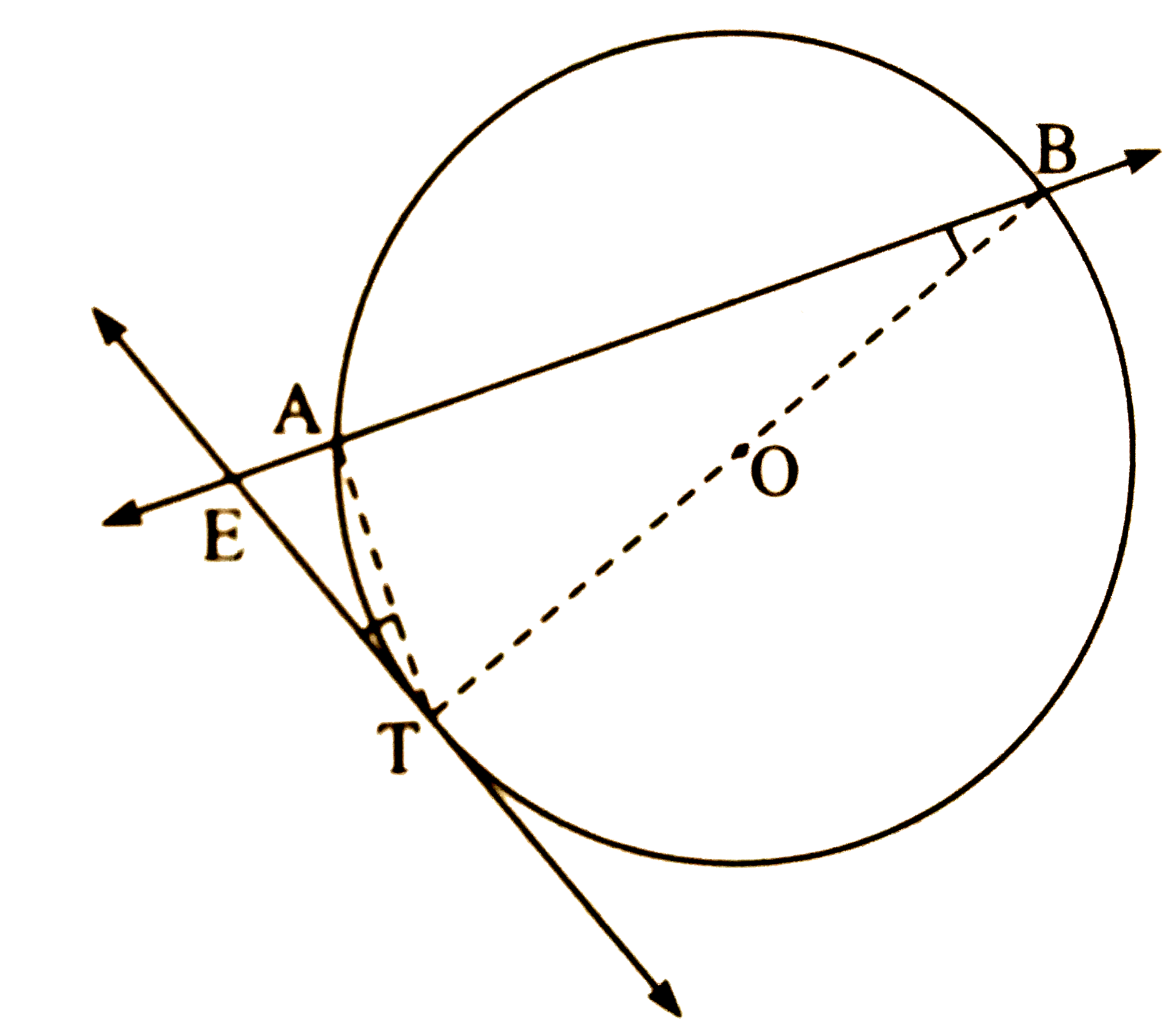 View Solution
View SolutionTwo circles touch each other externally at P. Two secants APB and CPD are drawn through P to meet the circle at A, C and B, D respectively. Then, which one of the following is correct ?
View SolutionIn the figure, two circles intersect each other at points A and B . C is a point on the smaller circle. Secant CA and secant CB of the smaller circle intersect the bigger circle at points D and E respectively then prove : seg DE ∣∣ line CF
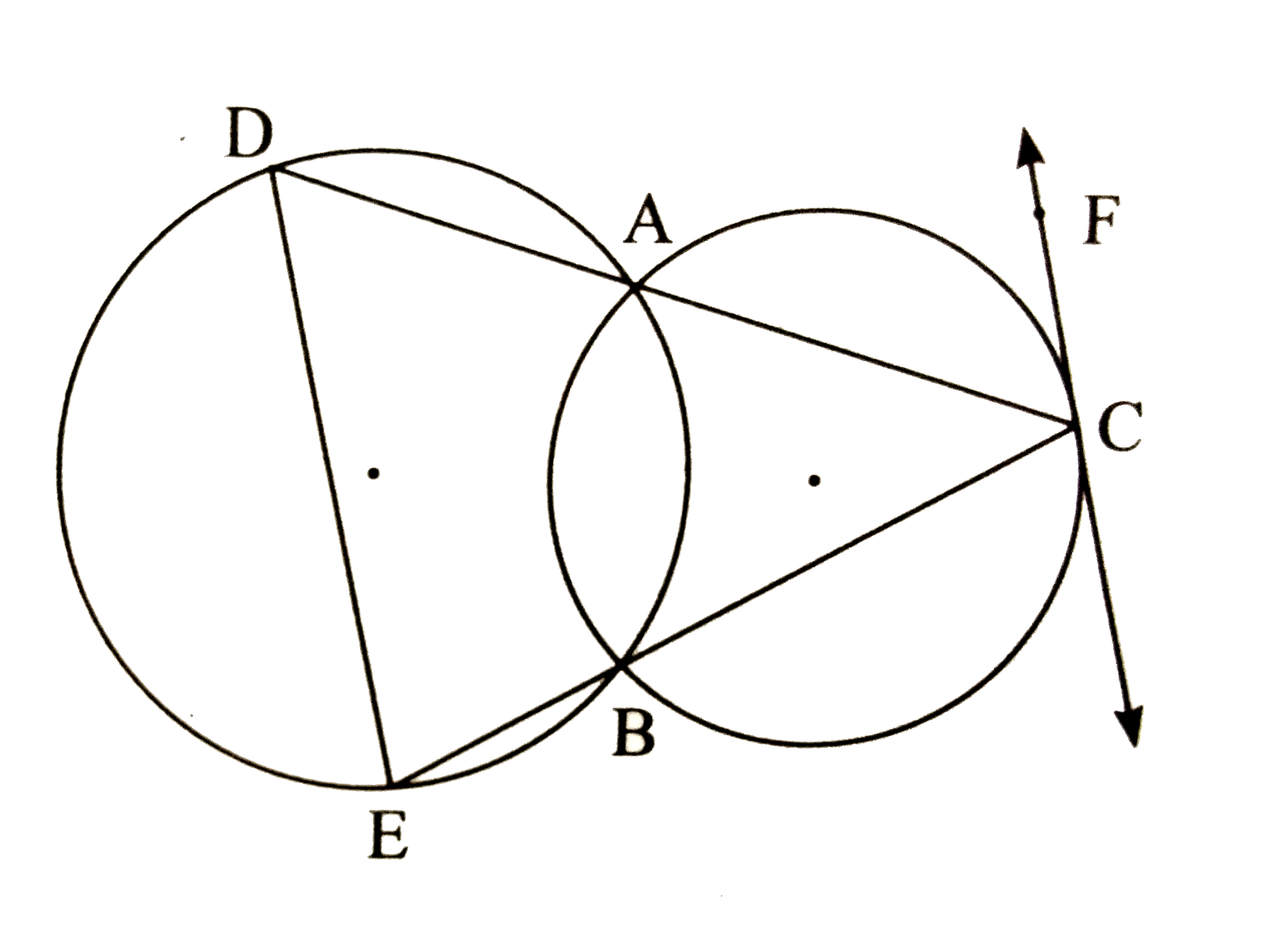 View Solution
View SolutionTANGENT : Intersection point of line and Circle are Coincident.
View SolutionTwo circles with equal radii are intersecting at the points (1,0) and (−1,0). Then tangent at the point (1,0) to one of the circles passes through the centre of the other circle.Then the distance between the centres of these circles is:
View Solution

