A vessel , whose bottom has round holes with diameter of 1mm is filled with water. Assuming that surface tension acts only at holes, find the maximum height to which the water can be filled in the vessel without leakage. Given that surface tension of water is 75×10−3N/m and g=10m/s2.
As shown in figure, here the vertical force due to surface tension at the hole Tcosθ×L=Tcosθ×2πr will balance the weight mg, i.e., πr2hρg,
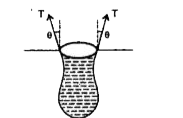
i.e., Tcosθ2πr=πr2hρg
or h=(2Tcosθ/ρrg) when θ=0, cosθ=1
Then h will be maximum.
So, (h)max=2×75×10−3103×5×10−4×10=0.03m=3cm
Similar Questions
A vessel whose bottom has round holes with diameter of 1 mm is filled with water Assuming that surface tension acts only at holes, then the maximum height to which the water can be filled in vessel without leakage is (given surface tension of water is 75×10−3N/m) and g=10m/s2
View SolutionA vessel, whose bottom has round holes with diameter of 0.1 mm , is filled with water. The maximum height to which the water can be filled without leakage is (S.T. of water =75 dyne/cm , g=1000 cm/s)
View Solution
Knowledge Check
A vessel whose bottom has round holes with diameter of 1 mm is filled with water Assuming that surface tenstion acts only at holes, then the maximum height to which the water can be filled in vessel without leakage is (given surface tension of water is 75×10−3N/m) and g=10m/s2
A3 cmB0.3 cmC3 mmD3 mA vessel, whose bottom has round holes with diameter of 0.1 mm , is filled with water. The maximum height to which the water can be filled without leakage is (S.T. of water =75 dyne/cm , g=1000 cm/s)
A100 cmB75 cmC50 cmD30 cmA vessel whose , bottom has round holes with diameter 0.1mm, is filled with water. The maximum height up to which water can be filled without leakage is
A100cmB75cmC50cmD30cm
A vessel whose , bottom has round holes with diameter 0.1mm, is filled with water. The maximum height up to which water can be filled without leakage is
View SolutionA vessel whose bottom has round holes with diameter of 1 mm is filled with water Assuming that surface tension acts only at holes, then the maximum height to which the water can be filled in vessel without leakage is (given surface tension of water is 75×10−3N/m) and g=10m/s2
View SolutionA large vessel having a very small circular hole of diameter 1 mm at the bottom is filled with water. Up to what maximum height (in cm) water can be filled in the vessel so that there is no leakage? [surface tension of water 7.5×10−2Nm−1andg=10ms−2]
View SolutionA container, whose bottom has round holes with diamter 0.1mm is filled with water. The maximum height in cm upto which water can be filled without leakage will be what? Surface tension =75×10−3N/m and g=10m/s2
View SolutionA vessel whose bottom has round holes with a diameter of d=0.1mm is filled with water. The maximum height of the water level h at which the water does not flow out, will be (The water does not wet the bottom of the vessel). [STofwater=70dyne/cm]
View Solution
