Given that →P+→Q=→Rand→R is perpendicular to →p. What is the angle between →pand→Q if |→p|=−→∣∣→R∣∣
A
3π4 rad
B
π4 rad
C
π rad
D
π2 rad
Text Solution
The correct Answer is:A
Here P=Rand∠ABC=90∘
∠A=∠C=45∘
At angle between →Pand→Q is alpha
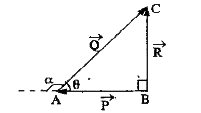
α=180−θ⇒135∘=34π rad
|
Similar Questions
Knowledge Check
The resultant of →P and →Q is perpendicular to →P. What is the angle between →P and →Q
Acos−1(P/Q)Bcos−1(−P/Q)Csin−1(P/Q)Dsin−1(−P/Q)If →P+→Q=→R & →R is perpendicular to →P.
define angle between →P & →Q if −→|P|=−→|R|−A3π4Bπ4CπDπ2If →P.→Q=PQ then angle between →P and →Q is
A0∘B30∘C45∘D60∘
If ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣ the angle between →Pand→Q is
View Solutionif →P+→Q=→P−→Q, then
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣ the angle between →Pand→Q is
View Solutionif →P+→Q=→P−→Q, then
View SolutionMagnitudes of vectors →P,→Q and →R are equal, If →P+→Q+→R=0, then angle between →Rand→Q is α while if →P+→Q=→R, the angle between →R and →P is β, then :
View Solution
