A bicycle is running straight towards north What is the locus of the centre of the front wheel of the bicycle whose diameter is d ?
A line parallel to the path of the wheel of the bicycle at a height d cm
A line parallel to the path of the wheel of the bicycle at a height d/2 cm
A circle of radius d/2 cm
A circle of radius d cm
To find the locus of the center of the front wheel of a bicycle moving straight towards the north, we can follow these steps:
1. Understand the Position of the Bicycle:
- The bicycle is moving straight towards the north. This means that the direction of motion is along a straight line pointing north.
2. Identify the Diameter of the Wheel:
- The diameter of the front wheel of the bicycle is given as d cm.
3. Calculate the Radius of the Wheel:
- The radius r of the wheel can be calculated as:
r=d2
- This radius is the distance from the center of the wheel to the ground.
4. Determine the Height of the Center of the Wheel:
- The center of the front wheel is located at a height equal to the radius above the ground. Therefore, the height of the center of the front wheel above the ground is d2 cm.
5. Define the Locus of the Center of the Front Wheel:
- As the bicycle moves straight towards the north, the center of the front wheel will trace a path parallel to the direction of motion (north) at a constant height of d2 cm above the ground.
- Thus, the locus of the center of the front wheel is a straight line.
6. Conclusion:
- The locus of the center of the front wheel of the bicycle is a straight line that is parallel to the path of the bicycle at a height of d2 cm.
Final Answer:
The locus of the center of the front wheel of the bicycle is a straight line parallel to the path of the wheel at a height of d2 cm above the ground.
---
- The bicycle is moving straight towards the north. This means that the direction of motion is along a straight line pointing north.
- The diameter of the front wheel of the bicycle is given as d cm.
- The radius r of the wheel can be calculated as:
r=d2
- This radius is the distance from the center of the wheel to the ground.
- The center of the front wheel is located at a height equal to the radius above the ground. Therefore, the height of the center of the front wheel above the ground is d2 cm.
- As the bicycle moves straight towards the north, the center of the front wheel will trace a path parallel to the direction of motion (north) at a constant height of d2 cm above the ground.
- Thus, the locus of the center of the front wheel is a straight line.
- The locus of the center of the front wheel of the bicycle is a straight line that is parallel to the path of the bicycle at a height of d2 cm.
The locus of the center of the front wheel of the bicycle is a straight line parallel to the path of the wheel at a height of d2 cm above the ground.
Similar Questions
What type of motion does the wheel of a bicycle have ?
View SolutionA wheel is mounted on frictionless central pivot and it can rotate freely in the vertical plane. There is a horizontal light rod fixed to the wheel below the pivot. There is a small sleeve of mass m which can slide along the rod without friction. The sleeve is connected to a light spring. The other end of the spring is fixed to the rim as shown. The sleeve is at the centre of the rod and the spring is relaxed. Now the wheel is held at rest and the sleeve is moved towards left so as to compress the sprig by some distance. The sleeve and the wheel are released simultaneously from this position.
(a) Is it possible that the wheel does not rotate as the sleeve perform SHM on the rod ?
(b) Find the value of spring constant k for situation described in (a) to be possible. The distance of rod from centre of the wheel is d.

View Solution
Knowledge Check
A bicycle is moving on a straight road at a constant speed. The wheels of the cycle exhibit :
ACircular, translational and periodic motionBCircular and translational motionCTranslational and periodic motionDCircular and periodic motionThe locus of the centre of a wheel rolling on a straight road is a ______
Aconcentric circleBstraight lineCcurve pathDparabolaA wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is vCM, then true statement is
 AThe velocity of point A is 2vCM and velocity of point B is zeroBThe velocity of point A is zero and velocity of point B is 2vCMCThe velocity of point A is 2vCM and velocity of point B is −vCMDThe velocities of both A and V are vCM
AThe velocity of point A is 2vCM and velocity of point B is zeroBThe velocity of point A is zero and velocity of point B is 2vCMCThe velocity of point A is 2vCM and velocity of point B is −vCMDThe velocities of both A and V are vCM
The rear wheel on a clown's bicycle has twice the radius of the front wheel. (a) When the bicycle is moving, is the linear speed at the very top of the rear wheel greater than, less than, or the same as that of the very top of the front wheel? (b) Is the angular speed of the rear wheel greater than, less than, or the same as that of the front wheel?
View SolutionA person rides a bicycle round a circular path of radius 50 m. The radius of the wheel of the bicycle is 50 cm. The cycle comes to the starting point for the first time in 1 hour. What is the number of revolutions of the wheel in 15 minutes ?
View SolutionA bit of mud stuck to a bicycle's front wheel of radius r detaches and is flung horizontally forward when it is at the top of the wheel. The bicycle is moving forward at a speed v and it is rolling without slipping. The horizontal distance travelled by the mud after detaching from the wheel is:
View SolutionA bicycle moves on a horizontal road with some acceleration. The forces of friction between the road and the front and rear wheels are F1 and F2 respectively.
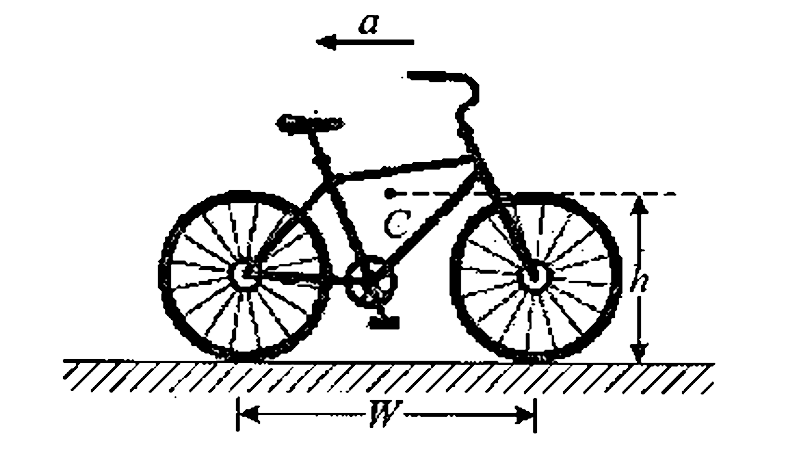
View SolutionA simplified model of a bicycle of mass M has two tires that each comes into contact with the ground at a point. The wheel base of this bicycle is JV, and the centre of mass C of the bicycle is located mid way between the tires and a height h above the ground.The bicycleis moving to the right,but slowing down at a constant acceleration a. Air resistance may be ignored. Assuming that the coefficient of sliding friction between each tyre and the ground is μ and that both tyres are skidding (sliding without rotating). Express your answer in terms of w,h,M and g .
What is the maximum value of a so that both tyres remain in contact with the ground ?
View Solution
