Three congruent circles each of radius 4 cm touch one another. What is the area (in cm)2 of the portion included between them?
8π
16√3−4π
16√3−4π
16√3−2π
To find the area of the portion included between three congruent circles each of radius 4 cm that touch one another, we can follow these steps:
Step 1: Understand the Configuration
The three circles are congruent and touch each other. The centers of these circles form an equilateral triangle. The distance between the centers of any two circles is equal to the sum of their radii.
Hint: Visualize the arrangement of the circles and their centers forming an equilateral triangle.
Step 2: Calculate the Side Length of the Triangle
Since each circle has a radius of 4 cm, the distance between the centers of any two circles (the side length of the equilateral triangle) is:
Side length=4 cm+4 cm=8 cm
Hint: Remember that the side length of the triangle is the sum of the radii of the two circles.
Step 3: Calculate the Area of the Equilateral Triangle
The area A of an equilateral triangle with side length a is given by the formula:
A=√34a2
Substituting a=8 cm:
A=√34×82=√34×64=16√3 cm2
Hint: Use the formula for the area of an equilateral triangle to find the area based on the side length.
Step 4: Calculate the Area of the Sector of Each Circle
The angle subtended by each sector at the center of the circles is 60∘ (since there are three circles, and they are evenly spaced around the triangle). The area of a sector of a circle is given by:
Area of sector=θ360×πr2
For r=4 cm and θ=60∘:
Area of sector=60360×π×42=16×π×16=8π3 cm2
Hint: Remember that the angle for each sector is 60∘ and apply the sector area formula.
Step 5: Calculate the Total Area of the Three Sectors
Since there are three circles, the total area of the three sectors is:
Total area of sectors=3×8π3=8π cm2
Hint: Multiply the area of one sector by the number of circles to find the total area of the sectors.
Step 6: Calculate the Area Included Between the Circles
The area included between the circles is the area of the equilateral triangle minus the total area of the sectors:
Area between circles=Area of triangle−Total area of sectors
Area between circles=16√3−8π cm2
Hint: Subtract the total area of the sectors from the area of the triangle to find the area between the circles.
Final Answer
The area of the portion included between the three circles is:
16√3−8π cm2
The three circles are congruent and touch each other. The centers of these circles form an equilateral triangle. The distance between the centers of any two circles is equal to the sum of their radii.
Since each circle has a radius of 4 cm, the distance between the centers of any two circles (the side length of the equilateral triangle) is:
Side length=4 cm+4 cm=8 cm
The area A of an equilateral triangle with side length a is given by the formula:
A=√34a2
Substituting a=8 cm:
A=√34×82=√34×64=16√3 cm2
The angle subtended by each sector at the center of the circles is 60∘ (since there are three circles, and they are evenly spaced around the triangle). The area of a sector of a circle is given by:
Area of sector=θ360×πr2
For r=4 cm and θ=60∘:
Area of sector=60360×π×42=16×π×16=8π3 cm2
Since there are three circles, the total area of the three sectors is:
Total area of sectors=3×8π3=8π cm2
The area included between the circles is the area of the equilateral triangle minus the total area of the sectors:
Area between circles=Area of triangle−Total area of sectors
Area between circles=16√3−8π cm2
The area of the portion included between the three circles is:
16√3−8π cm2
Similar Questions
Knowledge Check
Three equal circles of unit radius touch each other. Then, the area of the circles is
Aπ3(2+√3)3B2π3(2+√3PP2)C6π(2+√3)2D16π(2+√3)2A chord of the larger among two concentric circles is of length 10 cm and it is tangent to the smaller circle. What is the area (in cm ) of the annular portion between the two circles?
A5π2B25πC5πD10πTwo circles of radius 4 cm and 6 cm touch each other internally. What is the length (in cm) of the longest chord of the outer circle, which is also a tangent to inner circle?
A12√2B8√2C6√2D4√2
Four equal circles, each of radius 5cm, touch each other. Find the area included between them.
View SolutionFour equal circles each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them.
[Take π=3.14]

View SolutionThree circles of equal radius 'a' cm touch each other. The area of the shaded region is :
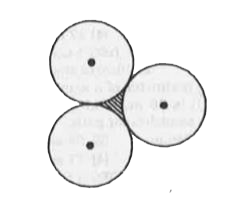
View SolutionThree circles of equal radius 'a' cm touch each other. The area of of the shaded region is :

View SolutionTwo circles of radius 4 cm and 6 cm touch each other internally. What is the length (in cm) of the longest chord of the outer circle, which is also a tangent to inner circle?
View Solution

