Four equal circles each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them.
[Take π=3.14]
![Four equal circles each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them. [Take pi=3.14]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RSA_MATH_X_C16_E01_037_Q01.png)
Video Solution
Text Solution
The correct Answer is:21.5cm2
Let A,B,C,D be the centres of these circles.
Join AB,BC,CD and DA.
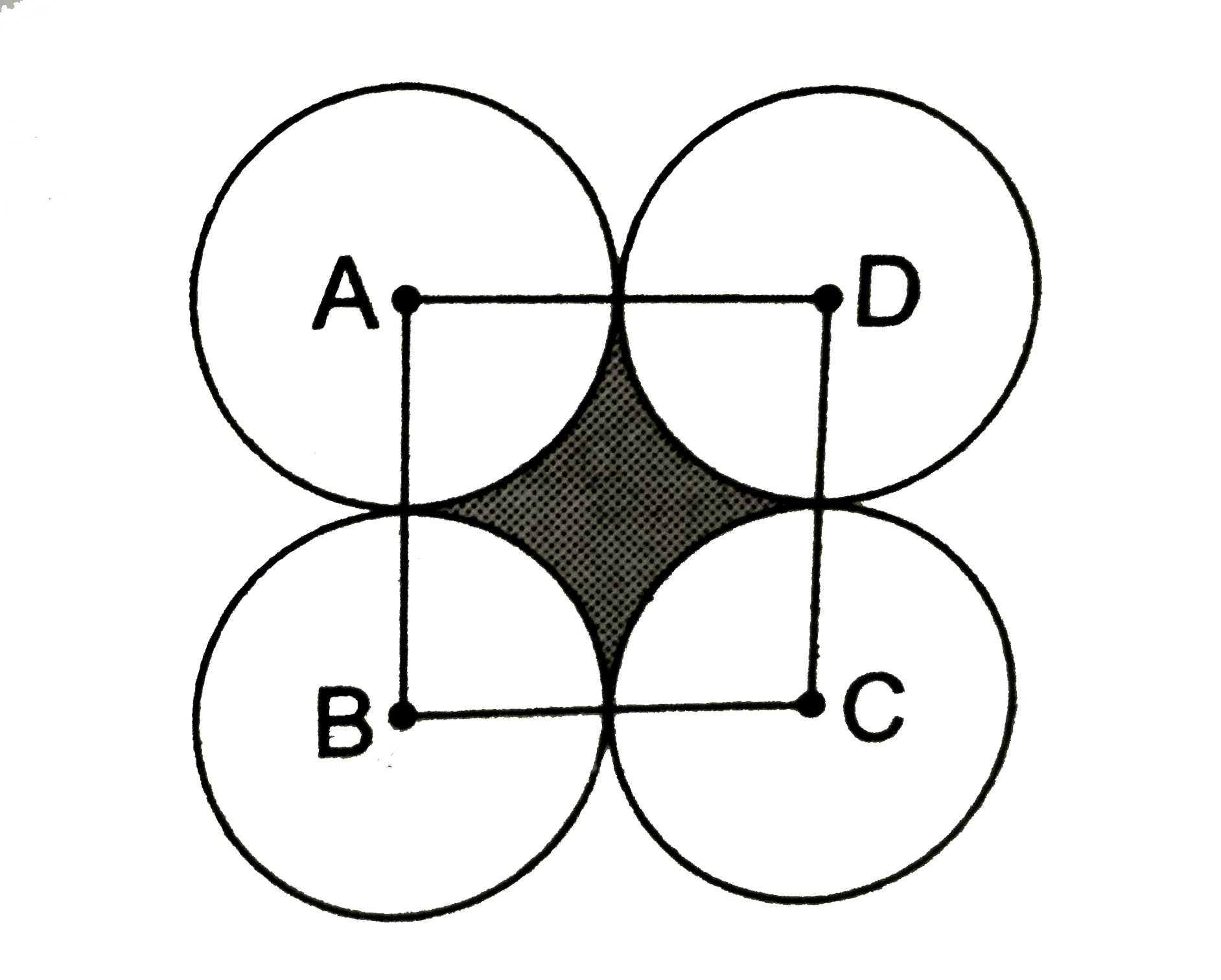
Required area =(area of the square ABCD with a=10 cm)
−4 (area of a sector with r=5cm,θ=90∘)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - EXERCISE1videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Exercise 16B51videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - SOLVED EXAMPLE_TYPE1videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
Similar Questions
Knowledge Check
- Question 1 - Select One
Three equal circles of unit radius touch each other. Then, the area of the circles is
Aπ3(2+√3)3B2π3(2+√3PP2)C6π(2+√3)2D16π(2+√3)2 - Question 2 - Select One
If the four equal circles of radius 3 cm touch each other externally, then the area of the region bounded by the four circles is
A4(9−π) sq. cmB9(4−π) sq. cm.C5(6−π) sq. cm.D6(5−π) sq. cm - Question 3 - Select One
Four equal circles each of radius 'a' units touch one another. The area enclose between them (π=227), in square units, is
A3a2B6a27C41a27Da27
Four equal circles, each of radius a , touch each other. Show that the area between them is 67a2 (Take π=22/7) .
View SolutionThree congruent circles each of radius 4 cm touch one another. What is the area (in cm)2 of the portion included between them?
View SolutionThree circles each of radius 3.5 cm touch one another. The area subtended between them is
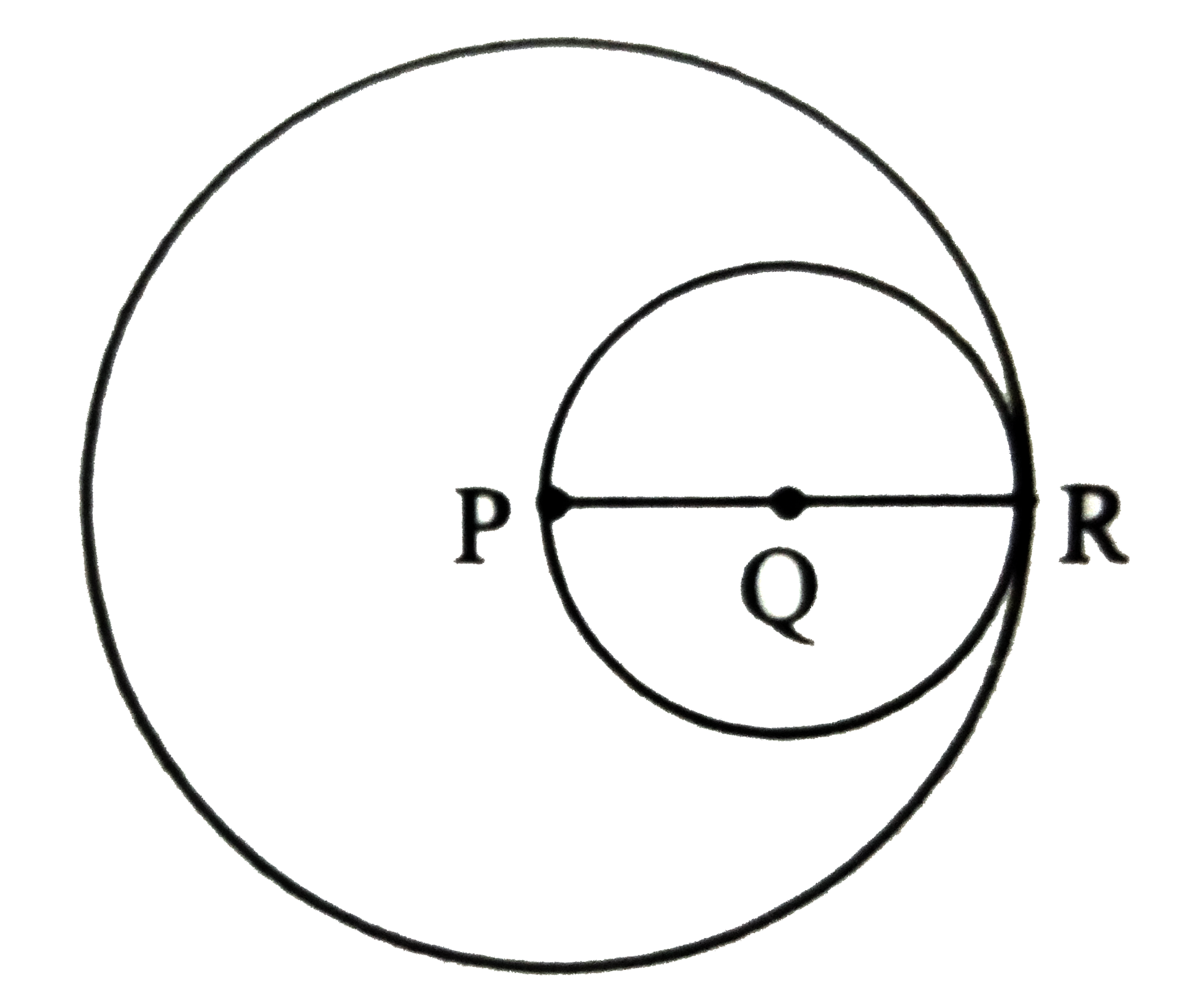
View SolutionTwo circles having radii 3.5cm and 4.8cm touch each other internally. Find the distance between their centres.
 View Solution
View SolutionTwo circles with radii 5cm and1.5 cm touch each other internally then find the distance between their centres.
View Solution


