समांतर चतुर्भुज ABCD के विकर्ण बिंदु O पर प्रतिच्छेद करते है। O से एक रेखा खींची गई है जो AD तथा BC को क्रमशः P तथा Q पर प्रतिच्छेदित करती है। सिद्ध कीजिए कि रेखाखण्ड PQ समांतर चतुर्भुज को दो बराबर क्षेत्रफल वाले भागों में विभाजित करती है ।
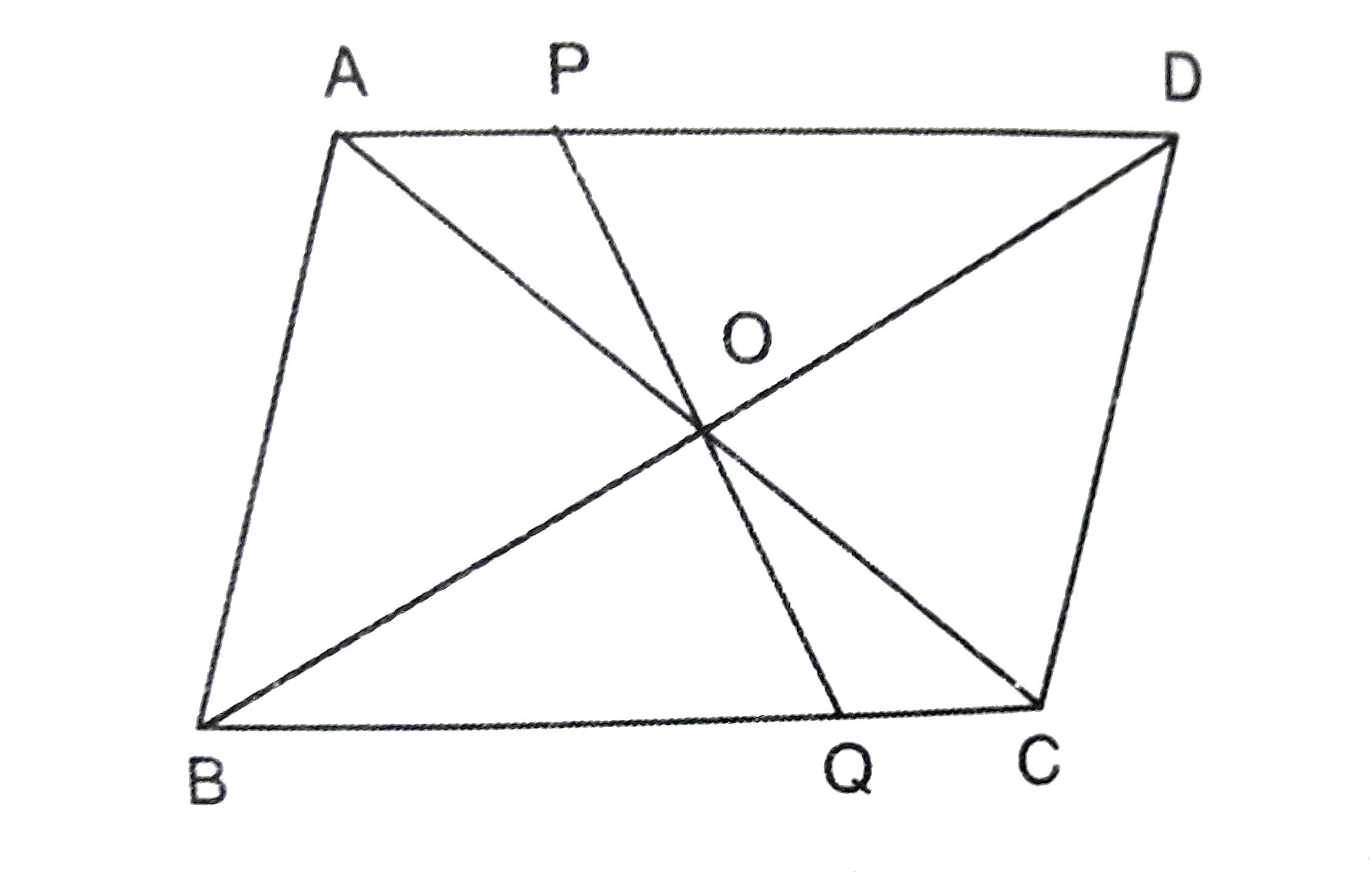
हमें सिद्ध करना है कि
ar(चतुर्भुज APQB)=ar(चतुर्भुज PQCD)=12(ar||gmABCD)
चूँकि चतुर्भुज के विकर्ण दो बराबर क्षेत्रफल वाली त्रिभुजों में विभाजित करता है।
∴ar(ΔABC)=ar(ACD)
⇒ar(चतुर्भुज ABQO)+ar(ΔCOQ)=ar(चतुर्भुज CDPO)ar(ΔAOP) ...(i)
ΔAOP तथा ΔCOQ पर विचार कीजिए। इन दोनों त्रिभुजों में
∠AOP=∠COQ [शीर्षाभिमुख कोण]
OA=OC [ ||gm के विकर्ण समद्विभाजित होते हैं]
तथा ∠OAP=∠OCQ [ एकान्तर कोण]
∴ΔAOP≅ΔCOQ
⇒ar(ΔAOP)=ar(ΔCOQ) ...(ii)
(i ) तथा (ii ) से
ar ( चतुर्भुज ABQO)+ar(ΔAOP)=ar( चतुर्भुज CDPO)+ar(ΔCOQ)
⇒ ar( चतुर्भुज ABQP) =(चतुर्भुज CDQP)
अथवा ar(चतुर्भुज APQB) =ar(चतुर्भुज PQCD)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - व्याख्यात्मक उदाहरण
1 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.1
6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionनिर्देशाक्षो को प्रारंभिक निर्देशांकों के समांतर रखते हुए मूल बिंदु को बिंदु P पर हटाने पर समीकरण ax+by+c=0 समीकरण ax+by+c+λ=0 के रूप में बदल जाता है सिद्ध कीजिए कि P बिन्दुपथ ax+by=λ होगा ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionनिम्न में से प्रत्येक कथन सत्य या असत्य है लिखिए और उत्तर का कारण भी लिखिए।
किसी वृत्त की स्पर्श रेखा वह है जो वृत्त को दो बिंदु पर प्रतिच्छेद करती है।
View Solutionदो बिंदुओं P और Q के स्थिति सदिश क्रमशः 2¯a+¯b और ¯a−2¯b है। एक बिंदु R का स्थिति सदिश ज्ञात कीजिए जो रेखा खण्ड PQ को 1:2 के अनुपात में अंतः तथा बाहृातः विभाजित करता है।
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionदीर्घवृत्त 3x2+5y2=32 के बिंदु P (2,2) पर खींची गई स्पर्श रेखा तथा अभिलम्ब, X-अक्ष को क्रमश: Q तथा R पर काटते है, तो ΔPQR का क्षेत्रफल (वर्ग इकाइयो में) है
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
View Solution
