ABCD is a parallelogram with AB and AD as adjacent sides. If ∠A=60∘ and AB = 2AD, then the diagonal BD will be equal to
√2 AD
√3 AD
2 AD
3 AD
To solve the problem, we will use the properties of a parallelogram and the cosine rule. Here are the steps to find the length of diagonal BD.
Step 1: Identify the given information
- ABCD is a parallelogram.
- ∠A=60∘
- AB=2AD
Let AD=x. Therefore, AB=2x.
Step 2: Apply the cosine rule
In triangle ABD, we can use the cosine rule to find BD:
BD2=AB2+AD2−2⋅AB⋅AD⋅cos(∠A)
Step 3: Substitute the known values
Substituting the values we have:
- AB=2x
- AD=x
- cos(60∘)=12
The equation becomes:
BD2=(2x)2+x2−2⋅(2x)⋅x⋅12
Step 4: Simplify the equation
Calculating each term:
BD2=4x2+x2−2x2
BD2=4x2+x2−x2
BD2=4x2
Step 5: Solve for BD
Taking the square root of both sides:
BD=√4x2=2x
Step 6: Substitute back the value of x
Since AD=x, we can express BD in terms of AD:
BD=2AD
Conclusion
Thus, the length of diagonal BD is equal to 2AD.
- ABCD is a parallelogram.
- ∠A=60∘
- AB=2AD
In triangle ABD, we can use the cosine rule to find BD:
BD2=AB2+AD2−2⋅AB⋅AD⋅cos(∠A)
Substituting the values we have:
- AB=2x
- AD=x
- cos(60∘)=12
BD2=(2x)2+x2−2⋅(2x)⋅x⋅12
Calculating each term:
BD2=4x2+x2−2x2
BD2=4x2+x2−x2
BD2=4x2
Taking the square root of both sides:
BD=√4x2=2x
Since AD=x, we can express BD in terms of AD:
BD=2AD
Thus, the length of diagonal BD is equal to 2AD.
Similar Questions
Knowledge Check
In a rhombus ABCD, ∠A=60∘, AB = 12cm. Then the diagonal BD is
A10 cmB2√3cmC6 cmD12 cmABCD is a rhombus whose side AB=4cmand ∠ABC=120∘, then the length of diagonal BD is equal to :
A1 cmB2 cmC3 cmD4 cm
A cyclic quadrilateral ABCD is such that AB=BC,AD=DC and AC and BD intersect at O. If ∠CAD=46∘, then the measure of ∠AOB is equal to:
View SolutionABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C=45∘, find ∠R.
View SolutionABCD is a parallelogram and bisector of angle A bisects BC at X. Show that AD= 2AB
View SolutionABCD is a parallelogram. E and F are mid-point of side AB and CD respectively. AF and CE intersect diagonal BD at P & Q respectively. If BD = 15 cm, find PQ.

View SolutionABCD is a rectangle. The diagonals AC and BD intersect at O. If AB = 32 cm and AD = 24 cm, then what is OD equal to ?
View SolutionABCD is a trapezium in which AB||CD and AD=BC (see figure). Show that
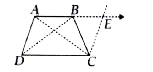
∠A=∠B
View Solution
