The point o is equidistant from the three sides of a triangle abc. Consider the following statements:
1. ∠OAC+∠OCB+∠OBA=90∘
2. ∠BOC=2∠BAC
3. The perpendiculars drawn from any point on OA to AB and AC are always equal Which of the above statements are correct ?
1 and 2 only
2 and 3 only
1 and 3 only
1,2 and 3
To solve the question, we need to analyze the statements regarding the point O, which is equidistant from the three sides of triangle ABC. This point O is known as the incenter of the triangle.
Step 1: Understanding the Incenter
The incenter of a triangle is the point where the angle bisectors of the triangle intersect. It is equidistant from all three sides of the triangle.
Step 2: Analyzing Statement 1
Statement 1: ∠OAC+∠OCB+∠OBA=90∘
- Since O is the incenter, we can express these angles in terms of the angles of triangle ABC.
- Let ∠A=∠BAC, ∠B=∠ABC, and ∠C=∠ACB.
- Then, we have:
∠OAC=12∠A,∠OCB=12∠C,∠OBA=12∠B
- Therefore, we can write:
∠OAC+∠OCB+∠OBA=12∠A+12∠B+12∠C=12(∠A+∠B+∠C)
- Since the sum of angles in a triangle is 180∘:
∠OAC+∠OCB+∠OBA=12×180∘=90∘
- Thus, Statement 1 is correct.
Step 3: Analyzing Statement 2
Statement 2: ∠BOC=2∠BAC
- The angle ∠BOC can be expressed in terms of the angles of triangle ABC.
- The relationship for the incenter gives us:
∠BOC=90∘+12∠A
- Therefore, for ∠BOC to equal 2∠BAC, we would need:
90∘+12∠A=2∠A
- Rearranging gives:
90∘=32∠A⇒∠A=60∘
- This is not true for all triangles, hence Statement 2 is incorrect.
Step 4: Analyzing Statement 3
Statement 3: The perpendiculars drawn from any point on OA to AB and AC are always equal.
- Since O is the incenter, the perpendiculars from O to the sides AB and AC are equal because they are both the radius of the incircle.
- Any point on OA will maintain this property due to the symmetry of the triangle and the properties of the incircle.
- Thus, Statement 3 is correct.
Conclusion
The correct statements are:
- Statement 1 is correct.
- Statement 2 is incorrect.
- Statement 3 is correct.
Final Answer
The correct statements are 1 and 3.
---
The incenter of a triangle is the point where the angle bisectors of the triangle intersect. It is equidistant from all three sides of the triangle.
Statement 1: ∠OAC+∠OCB+∠OBA=90∘
- Let ∠A=∠BAC, ∠B=∠ABC, and ∠C=∠ACB.
- Then, we have:
∠OAC=12∠A,∠OCB=12∠C,∠OBA=12∠B
- Therefore, we can write:
∠OAC+∠OCB+∠OBA=12∠A+12∠B+12∠C=12(∠A+∠B+∠C)
- Since the sum of angles in a triangle is 180∘:
∠OAC+∠OCB+∠OBA=12×180∘=90∘
- Thus, Statement 1 is correct.
Statement 2: ∠BOC=2∠BAC
- The relationship for the incenter gives us:
∠BOC=90∘+12∠A
- Therefore, for ∠BOC to equal 2∠BAC, we would need:
90∘+12∠A=2∠A
- Rearranging gives:
90∘=32∠A⇒∠A=60∘
- This is not true for all triangles, hence Statement 2 is incorrect.
Statement 3: The perpendiculars drawn from any point on OA to AB and AC are always equal.
- Any point on OA will maintain this property due to the symmetry of the triangle and the properties of the incircle.
- Thus, Statement 3 is correct.
The correct statements are:
- Statement 1 is correct.
- Statement 2 is incorrect.
- Statement 3 is correct.
The correct statements are 1 and 3.
Similar Questions
Consider the following statements :
1. The perimeter of a triangle is greater than the sum of its three medians.
2. In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.
Which of the above statements is/are correct?View SolutionIn the figure given below, ABC is a triangle with AB = BC and D is an interior point of the triangle ABC such that ∠DAC=∠DCA.

Consider the following statements :
1. Triangle ADC is an isosceles triangle.
2. Dis the centroid of the triangle ABC.
3. Triangle ABD is congruent to the triangle CBD.
Which of the above statements are correct ?View Solution
Knowledge Check
- Question 1 - Select One
Consider the following statement :
1. There exixts no triangle ABC for which sin A + sin B = sin C.
2. If the angle of a triangle are in the ratio 1 : 2 : 3, then its sides will be in the ratio 1:√3:2.
Which of the above statement is/are correct?A1 onlyB2 onlyCBoth 1 and 2DNeither 1 nor 2 - Question 2 - Select One
Consider the following statements in respect of the points (p,p-3),(q+3,q) and (6,3) :
1. The points lie on a straight line.
2. The points always lie in the first quadrant only for any value of p and q.
Which of the above statements is/are correct?A1 onlyB2 onlyCBoth 1 and 2DNeither 1 nor 2
P is any point in the angle ABC such that the perpendiculars drawn from P on AB and BC are equal. Prove that BP bisects angle ABC.
View SolutionConsider the following statements in respect of an equilateral triangle ABC.
1. The altitudes are congruent.
2. The three medians are congruent.
3. The centroid bisects the altitude.
Which of the above statements is/are correct ?View SolutionConsider the following statements :
1. The point of intersection of the perpendicular bisectors of the sides of a triangle may lie outside the triangle.
2. The point of intersection of the perpendiculars drawn from the vertices to the opposite sides of a triangle may lie on two sides.
Which of the above statements is/are correct ?View Solution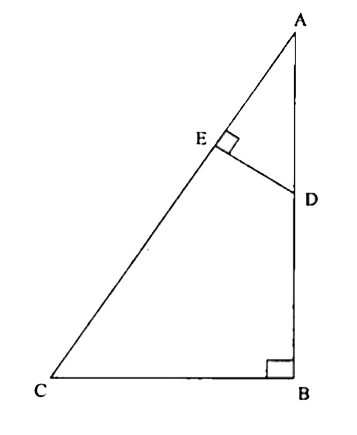
In the figure given above ∠ABC=∠AED=90∘
Consider the following statements :
1. ABC and ADE are similar triangles.
2. The four points B, C,E and D may lie on a circle.
Which of the above statements is/are correct ?View SolutionConsider the following statements :
1. The number of circles that can be drawn through three non-collinear points is infinity.
2. Angle formed in minor segment of a circle is acute.
Which of the above statements is/are correct?View SolutionABC is a triangle and D is the mid-point of BC . The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
View Solution

