Which of the points P(5, -1), Q(3, -2) and R(1, 1) lie in the solution of the system of inequations x+y≤4 and x−y≥2?
Q and R only
P and R only
P and Q only
P, Q and R
To determine which of the points P(5, -1), Q(3, -2), and R(1, 1) lie in the solution of the system of inequalities x+y≤4 and x−y≥2, we will evaluate each point against both inequalities.
Step 1: Check Point P(5, -1)
1. Evaluate the first inequality:
x+y≤4
Substitute x=5 and y=−1:
5+(−1)=4≤4(True)
2. Evaluate the second inequality:
x−y≥2
Substitute x=5 and y=−1:
5−(−1)=5+1=6≥2(True)
Conclusion for Point P: Point P(5, -1) satisfies both inequalities.
Step 2: Check Point Q(3, -2)
1. Evaluate the first inequality:
x+y≤4
Substitute x=3 and y=−2:
3+(−2)=1≤4(True)
2. Evaluate the second inequality:
x−y≥2
Substitute x=3 and y=−2:
3−(−2)=3+2=5≥2(True)
Conclusion for Point Q: Point Q(3, -2) satisfies both inequalities.
Step 3: Check Point R(1, 1)
1. Evaluate the first inequality:
x+y≤4
Substitute x=1 and y=1:
1+1=2≤4(True)
2. Evaluate the second inequality:
x−y≥2
Substitute x=1 and y=1:
1−1=0≥2(False)
Conclusion for Point R: Point R(1, 1) does not satisfy the second inequality.
Final Conclusion:
- Points P(5, -1) and Q(3, -2) lie in the solution of the system of inequalities.
- Point R(1, 1) does not lie in the solution.
x+y≤4
Substitute x=5 and y=−1:
5+(−1)=4≤4(True)
x−y≥2
Substitute x=5 and y=−1:
5−(−1)=5+1=6≥2(True)
x+y≤4
Substitute x=3 and y=−2:
3+(−2)=1≤4(True)
x−y≥2
Substitute x=3 and y=−2:
3−(−2)=3+2=5≥2(True)
x+y≤4
Substitute x=1 and y=1:
1+1=2≤4(True)
x−y≥2
Substitute x=1 and y=1:
1−1=0≥2(False)
- Points P(5, -1) and Q(3, -2) lie in the solution of the system of inequalities.
- Point R(1, 1) does not lie in the solution.
Similar Questions
Knowledge Check
The solution of the system of equations 3x+2y≤12,x≥1,y≤2 is
A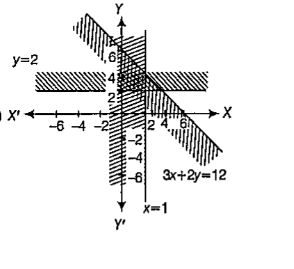 B
B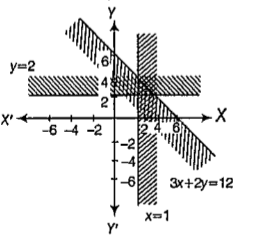 C
C DNone of the above
DNone of the aboveThe solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
A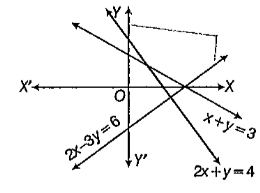 B
B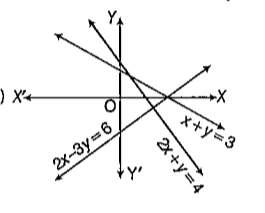 C
C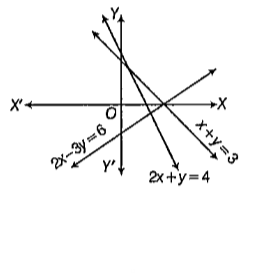 D
D
The graphical solution of the system of linear inequalities 3x,4y≥12,y≥1,x≥0 is
A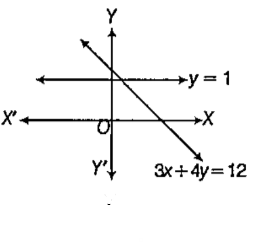 B
B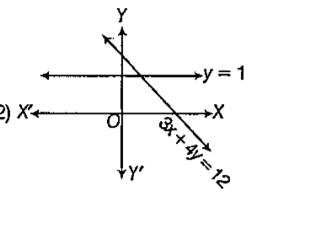 C
C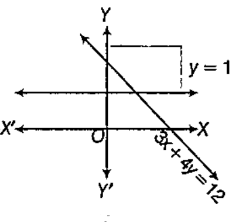 D
D
Draw the graph of the solution set of the inequation 2x−y≥1
View SolutionSolve the inequations 3x+2y≤15,4x−3y≥4andx≥0.
View SolutionThe region represented by the solution of system of inequalities 5x+4y≤40,x≥2,y≥3 is
View SolutionThe graphical solution of linear inequalities x+y≥5 and x−y≤3,
View SolutionThe region represented by the solution set of the system of inequalities x−y≤1,x+2y≤8,2x+y≥2,0,y≥0is
View Solution
