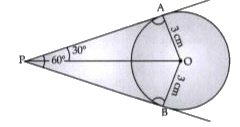
If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then what is the length of each tangent ?
6 cm
cm
To find the length of each tangent drawn to a circle from a point outside the circle, we can follow these steps:
1. Understand the Geometry:
We have a circle with a radius of 3 cm and two tangents (AB and AC) that meet at an external point A, forming an angle of 60° between them.
2. Draw the Diagram:
Draw the circle with center O. Mark the points where the tangents touch the circle as B and C. The angles at point A (∠BAC) is given as 60°.
3. Identify Right Angles:
The radius drawn to the point of tangency (OB and OC) is perpendicular to the tangent lines (AB and AC). Thus, ∠OBA = 90° and ∠OCA = 90°.
4. Use the Angle Bisector Theorem:
Since the angle ∠BAC is 60°, the angles ∠BAO and ∠CAO are each 30° (because they are equal and sum to 60°).
5. Apply Trigonometry:
In triangle OAB, we can use the tangent function:
tan(30°)=OBAB
Here, OB is the radius (3 cm), and AB is the length of the tangent we want to find.
6. Substitute the Values:
The value of tan(30°) is 1√3. Therefore, we can write:
1√3=3AB
7. Cross-Multiply to Solve for AB:
Cross-multiplying gives:
AB=3√3
8. Conclusion:
Since both tangents (AB and AC) are equal in length, the length of each tangent is:
Length of each tangent=3√3 cm
Final Answer:
The length of each tangent is 3√3 cm.
---
We have a circle with a radius of 3 cm and two tangents (AB and AC) that meet at an external point A, forming an angle of 60° between them.
Draw the circle with center O. Mark the points where the tangents touch the circle as B and C. The angles at point A (∠BAC) is given as 60°.
The radius drawn to the point of tangency (OB and OC) is perpendicular to the tangent lines (AB and AC). Thus, ∠OBA = 90° and ∠OCA = 90°.
Since the angle ∠BAC is 60°, the angles ∠BAO and ∠CAO are each 30° (because they are equal and sum to 60°).
In triangle OAB, we can use the tangent function:
tan(30°)=OBAB
Here, OB is the radius (3 cm), and AB is the length of the tangent we want to find.
The value of tan(30°) is 1√3. Therefore, we can write:
1√3=3AB
Cross-multiplying gives:
AB=3√3
Since both tangents (AB and AC) are equal in length, the length of each tangent is:
Length of each tangent=3√3 cm
The length of each tangent is 3√3 cm.
Similar Questions
Knowledge Check
If two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3cm then the length of each tangent is
A3cmB3√32cmC3√3cmD6cmIF two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to
A3√32 cmB6 cmC3 cmD3√3cmIf two tangents inclined at an angle of 60∘ are drawn to a circle of radius 4 cm, then the length of each tangent is equal to :
A2√3 cmB8 cmC4 cmD4√3 cm
If two tangents inlined at an angle 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to :
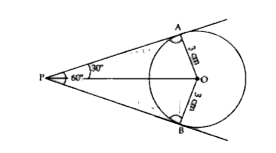
View SolutionIf two tangents are inclined at 60∘ are drawn to a circle of radius 3cm then find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.
View SolutionTwo tangents making an angle of 1200 with each other are drawn to a circle of radius 6cm, then the length of each tangent is equal to √3 cm (b) 6 √3 cm (c) √2 cm (d) 2 √3 cm
View SolutionTwo tangents making an angle of 60∘ between them, are drawn to a circle of radius √2 cm, then find the length of each tangent.
View SolutionIn From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
View Solution