Three vectors of equal magnitude are shown in figure. Find angle θ formed by →a+→b−→c with x-axis, tan(θ) = ? 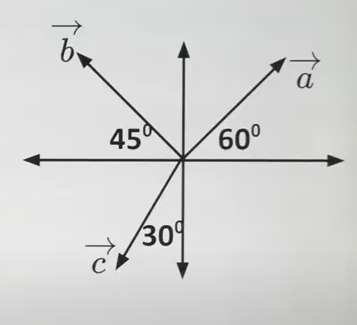
√6+1√2−1
√6−1√2+1
1√2
√2−1√6+1
Step by step video & image solution for Three vectors of equal magnitude are shown in figure. Find angle theta formed by vec(a) + vec(b) - vec(c) with x-axis, tan(theta) = ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Let →a,→b,→c be three mutually perpendicular vectors of the same magnitude and equally inclined at an angle θ, with the vector →a+→b+→c. The 36cos22θ is equal to __________ .
View SolutionThe sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.
View Solution.Vectors →A,→B and →c are shown in figure.Find angle between (i) →A and →B. (ii) →A and →C. ,(iii)vec Bandvec C
View SolutionIf →a and →b are vectors of equal magnitude, write the value of (→a+→b).→a−→b.
View SolutionIf →a, →b, →c are three mutually perpendicular vectors of equal magniltgude, prove that →a+→b+→c is equally inclined with vectors →a, →b, and →⋅ also find the angle.
View Solution→A and →B are two vectors of equal magnitude and θ is angle between them the angle between →A and →B with their resultant is
View SolutionIf unit vectors ˆa and ˆb are inclined at angle θ, then prove that
∣∣→a−→b∣∣=2sin.θ2.
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionIf →a,→b,→c are vectors of equal magnitudes and each of them inclined of 60∘ each others. If ∣∣→a+→b+→c∣∣=√6, then find |→a|.
View SolutionThe resultant of two velocity vectors →A and →B is perpendicular to →A. Magnitude of Resultant →R is equal to half magnitude of →B. If the angle between →A and →B is (30θ)∘, then value of θ is ?
View Solution
