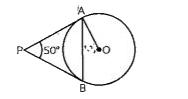
PA and PB are the tangent on a circle with centre O such that ∠APB=42∘. What will be the value of ∠AOB?
84∘
116∘
138∘
124∘
The correct Answer is:C
To solve the problem, we need to find the value of angle AOB given that PA and PB are tangents to the circle at points A and B respectively, and that angle APB is 42 degrees.
1. Understanding the Geometry:
- We have a circle with center O.
- Points A and B are points of tangency where the tangents PA and PB touch the circle.
- By the property of tangents, the radius at the point of tangency is perpendicular to the tangent line. Therefore, OA ⊥ PA and OB ⊥ PB.
2. Identifying Angles:
- Since OA is perpendicular to PA, angle OAP = 90 degrees.
- Similarly, since OB is perpendicular to PB, angle OBP = 90 degrees.
- We know that angle APB = 42 degrees.
3. Using the Angles in Triangle APB:
- The angles in triangle APB can be expressed as:
- Angle OAP + Angle APB + Angle OBP = 180 degrees.
- Substituting the known values:
- 90 degrees + 42 degrees + 90 degrees = 180 degrees.
4. Finding Angle AOB:
- The angle AOB can be found using the fact that the angles around point P add up to 360 degrees:
- Angle AOB + Angle APB = 180 degrees (since they are supplementary).
- Therefore, we can calculate angle AOB:
- Angle AOB = 180 degrees - Angle APB
- Angle AOB = 180 degrees - 42 degrees
- Angle AOB = 138 degrees.
5. Final Answer:
- Thus, the value of angle AOB is 138 degrees.
- We have a circle with center O.
- Points A and B are points of tangency where the tangents PA and PB touch the circle.
- By the property of tangents, the radius at the point of tangency is perpendicular to the tangent line. Therefore, OA ⊥ PA and OB ⊥ PB.
- Since OA is perpendicular to PA, angle OAP = 90 degrees.
- Similarly, since OB is perpendicular to PB, angle OBP = 90 degrees.
- We know that angle APB = 42 degrees.
- The angles in triangle APB can be expressed as:
- Angle OAP + Angle APB + Angle OBP = 180 degrees.
- Substituting the known values:
- 90 degrees + 42 degrees + 90 degrees = 180 degrees.
- The angle AOB can be found using the fact that the angles around point P add up to 360 degrees:
- Angle AOB + Angle APB = 180 degrees (since they are supplementary).
- Therefore, we can calculate angle AOB:
- Angle AOB = 180 degrees - Angle APB
- Angle AOB = 180 degrees - 42 degrees
- Angle AOB = 138 degrees.
- Thus, the value of angle AOB is 138 degrees.
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
A36∘B18∘C27∘D36∘ - Question 2 - Select One
Two tangents PA and PB are drawn to a circle of centre O in such a way that ∠AOB=120∘. Calculate the value of ∠APB.
 A40°B50°C60°D80°
A40°B50°C60°D80° - Question 3 - Select One
If PA and PB are two tangents to a circle with centre O such that ∠APB=80∘, then, ∠AOP=?
A40∘B50∘C60∘D70∘
If PA and PB are tangents drawn from an external point P to a circle with centre O such that ∠APB=70∘, then ∠OAB is equal to:
यदि PA और PB एक बाहरी बिंदु P से केंद्र O के साथ एक वृत्त में खींची गई स्पर्श रेखाएँ हैं जैसे कि ∠APB=70∘ तो ∠OAB बराबर है:View SolutionIn Fig AP and BP are tangents to a circle with centre O, such that AP = 5 cm , and ∠APB=60∘ . Find the length of chord AB.
 View Solution
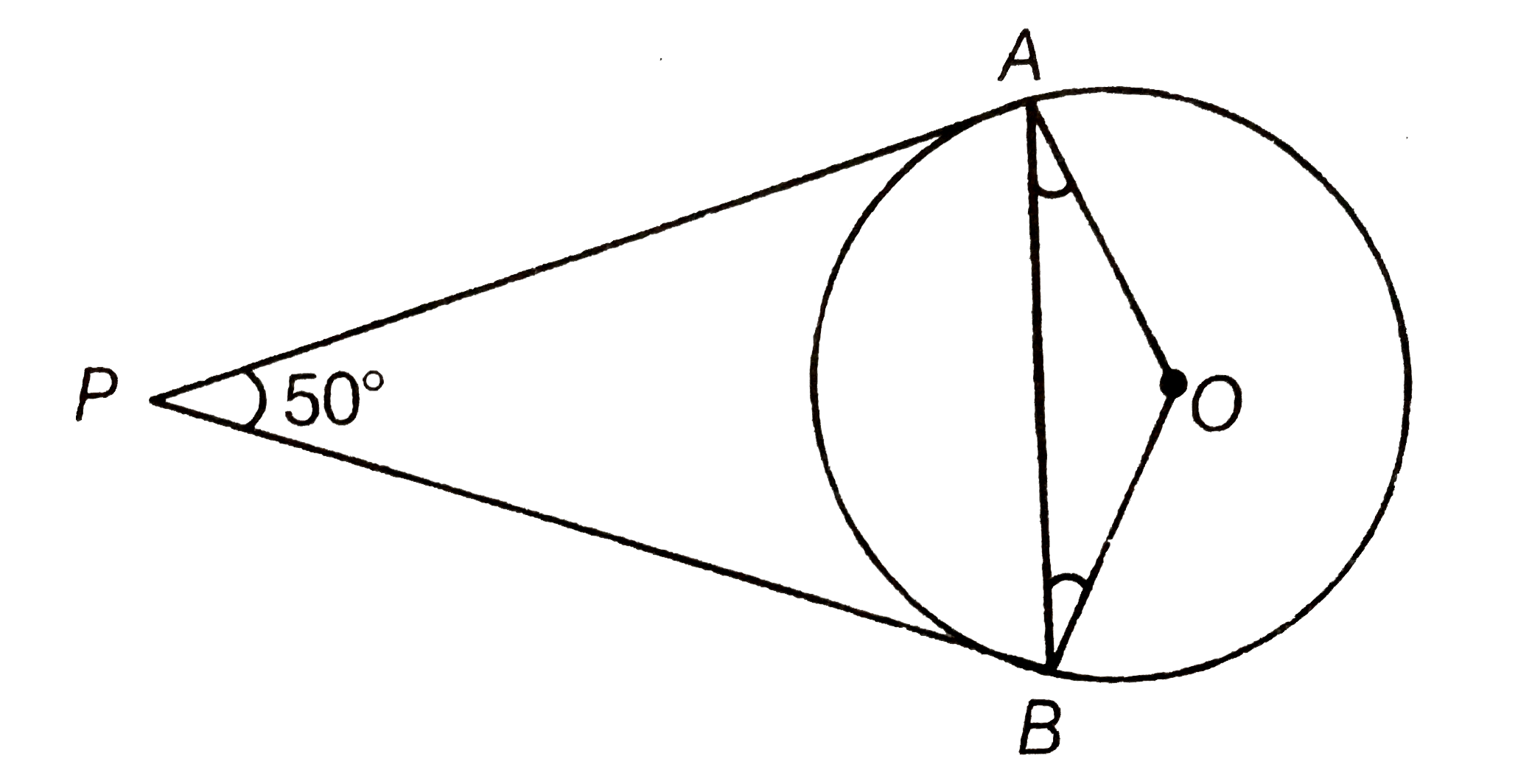
View SolutionIf PA and PB are tangents to the circle with centre O such that ∠APB=50∘ then ∠OAB is equal to
View SolutionIn the given figure, AP and BP are tangents to a circle with centre O. IF ∠APB=62∘ then the measure of ∠AQB is
 View Solution
View SolutionIn figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
 View Solution
View Solution