A wire is bent in the form fo uniform circular ring. A and B are two points on the ring such that ∠AOB=60∘ , where O is the centre of ring . If the equivalent resistance cross A and B is 5 . What is the resistance of whole wire
5
6
30
36
The correct Answer is:D
Similar Questions
In a uniform ring of resistance R there are two points A and B such that ∠ACB=θ, where C is the centre of the ring. The equivalent resistance between A and B is
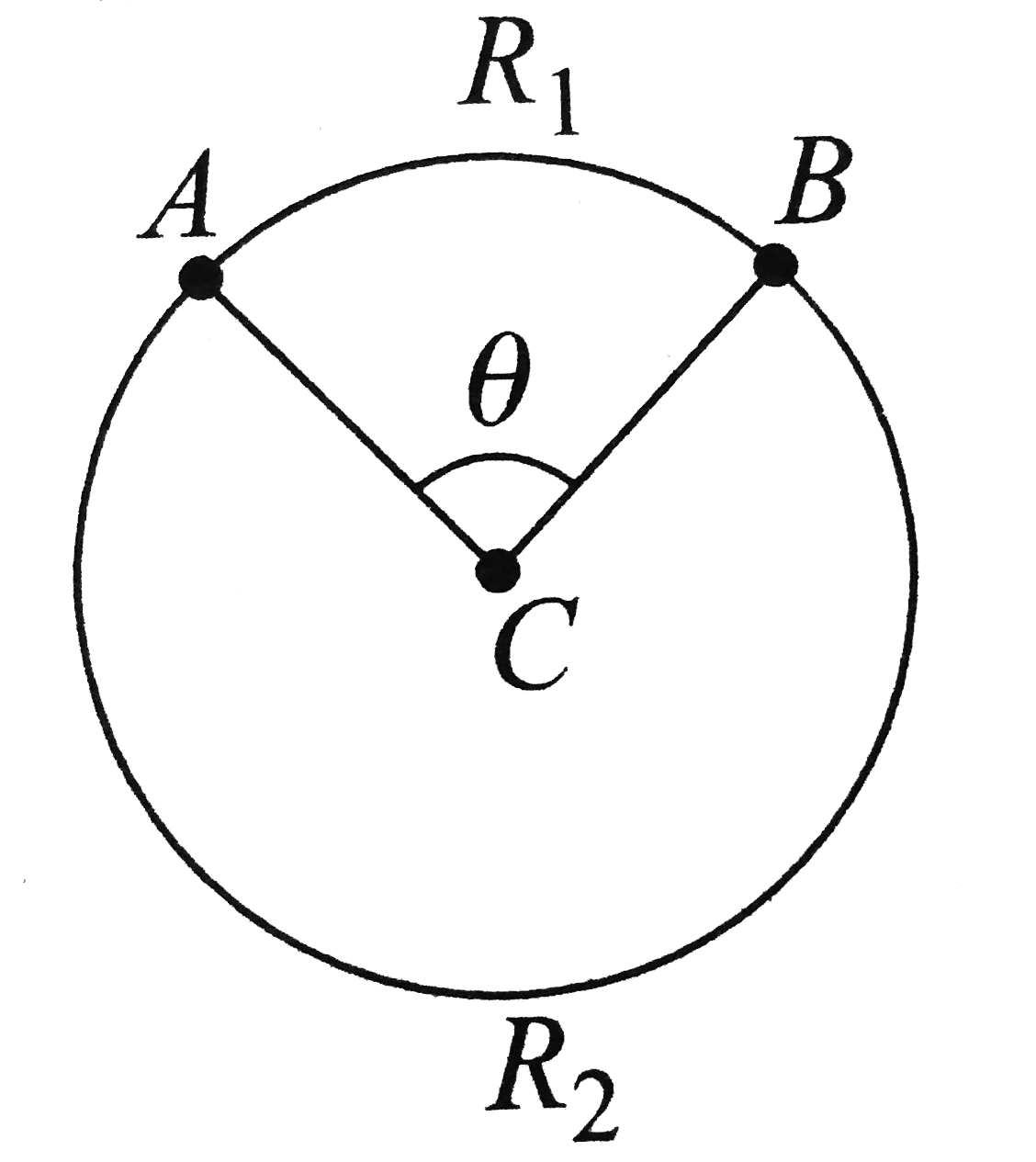
View SolutionA uniform wire of resistance =3Ω and length l is stretched to double its length. Now it is bent to form a circular loop and two point P&Q lies on the loop such that they subtend 60∘ angle at centre. The equivalent resistance between two point P & Q is:
View Solution
Knowledge Check
A and B are two points on a uniform ring of resistance R. The ∠ACB=90∘, where C is the center of the ring. The equivalent resistance between A and B is.
A3R4B3R8C3R16D3R32In a uniform ring of resistance R there are two points A and B such that ∠ACB=θ, where C is the centre of the ring. The equivalent resistance between A and B is
 ARθ2πBR(1−θ2π)CRθ(2π−θ)4π2DR(2π−θ)4π2
ARθ2πBR(1−θ2π)CRθ(2π−θ)4π2DR(2π−θ)4π2A and B are two points on a uniform ring of resistance R the ∠ASCB=θ, whre C is the centre of the sign. The equivalent reisrtance between A and b
AR4π2(2π−θ)θBR(I−θ2π)CRθ2πDR2π−θ4π
A wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
View SolutionA and B are two points on a uniform ring of resistance 15Ω. The <AOB=45∘ The equivalent resistance between A and B is
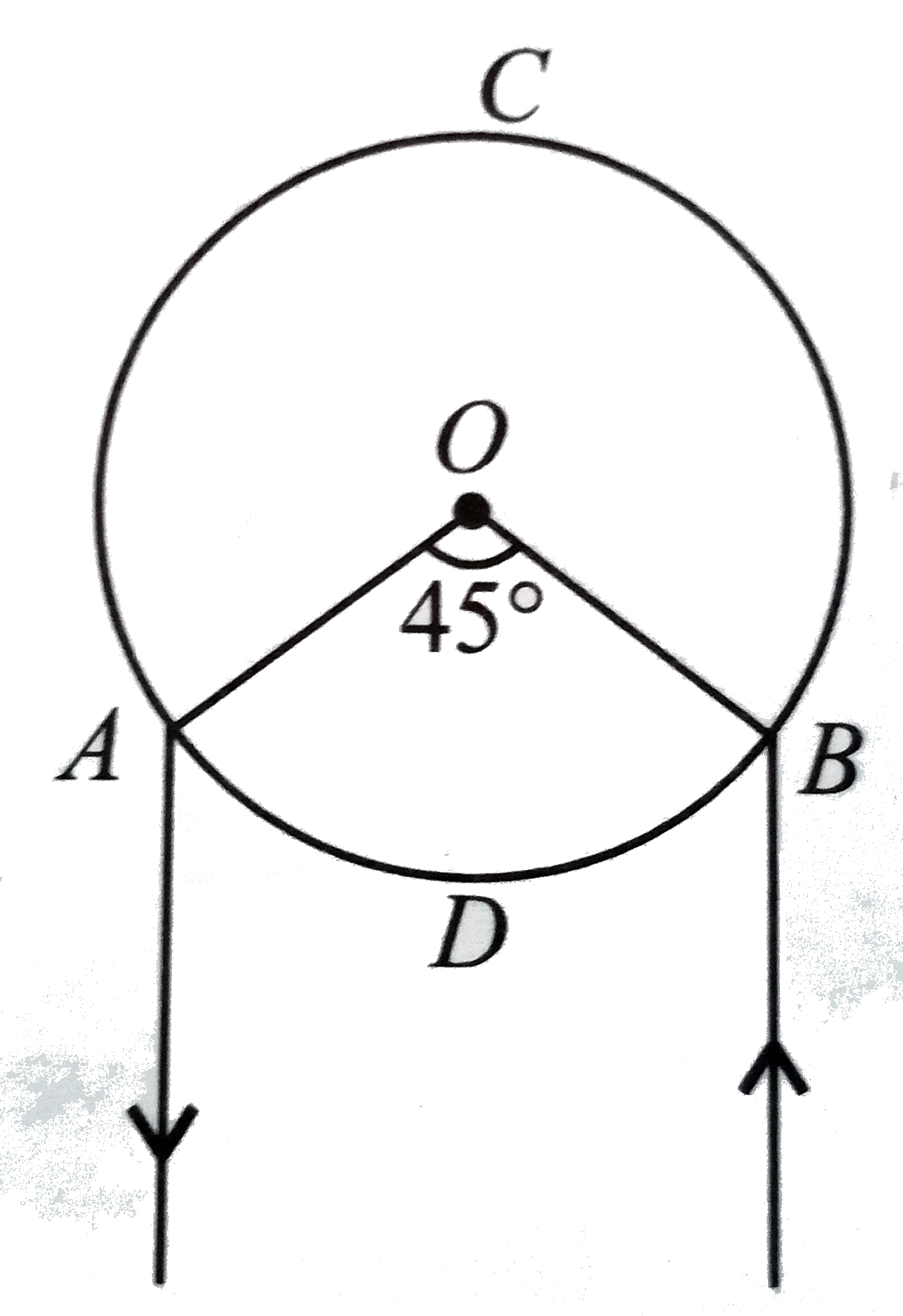
View SolutionA uniform wire of resistance =3Ω and length l is stretched to double its length. Now it is bent to form a circular loop and two point P&Q lies on the loop such that they subtend 60∘ angle at centre. The equivalent resistance between two point P & Q is:
View SolutionA wire of mass 'm' and length 'l' is bent in the form of a circular ring. The moment of inertia of the ring about its axis is-
View SolutionA Wire of resistance 12 ohm is bent in the form of a circular ring. The effective resistance between the two points on any diameter of the circle is :
View Solution
