A uniform wire of resistance =3Ω and length l is stretched to double its length. Now it is bent to form a circular loop and two point P&Q lies on the loop such that they subtend 60∘ angle at centre. The equivalent resistance between two point P & Q is:
53Ω
12Ω
35Ω
112Ω
The correct Answer is:A
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
Step 1: Determine the new length and area of the wire after stretching
The original length of the wire is L and the original resistance is R=3Ω. When the wire is stretched to double its length, the new length L′ becomes:
L′=2L
Since the volume of the wire remains constant, we have:
A⋅L=A′⋅L′
where A is the original cross-sectional area and A′ is the new cross-sectional area. Therefore:
A⋅L=A′⋅(2L)⟹A′=A2
Step 2: Calculate the new resistance of the stretched wire
The resistance R′ of the wire after stretching can be calculated using the formula:
R′=ρL′A′
Substituting L′=2L and A′=A2:
R′=ρ2LA2=ρ4LA
Since the original resistance R is given by:
R=ρLA=3Ω
we can substitute this into the equation for R′:
R′=4⋅R=4⋅3=12Ω
Step 3: Form a circular loop and determine the arc length
When the wire is bent to form a circular loop, the total length of the wire is equal to the circumference of the circle:
C=2πr=2L
From this, we can find the radius r:
r=Lπ
Step 4: Calculate the length of the arc between points P and Q
The angle subtended by points P and Q at the center is 60∘ or π3 radians. The length of the arc PQ can be calculated as:
Length of arc PQ=r⋅θ=r⋅π3=Lπ⋅π3=L3
Step 5: Calculate the resistance of the arc PQ
The resistance R1 of the arc PQ is proportional to its length:
R1=R′⋅Length of arc PQC=12Ω⋅L32L=12Ω⋅16=2Ω
Step 6: Calculate the resistance of the remaining part of the loop
The remaining length of the wire (the rest of the loop) is:
Remaining length=2L−L3=6L3−L3=5L3
The resistance R2 of this remaining part is:
R2=R′⋅Remaining lengthC=12Ω⋅5L32L=12Ω⋅56=10Ω
Step 7: Calculate the equivalent resistance between points P and Q
The resistances R1 and R2 are in parallel:
1Req=1R1+1R2=12+110
Finding a common denominator (10):
1Req=510+110=610=35
Thus,
Req=53Ω
Final Answer
The equivalent resistance between points P and Q is:
53Ω
The original length of the wire is L and the original resistance is R=3Ω. When the wire is stretched to double its length, the new length L′ becomes:
L′=2L
Since the volume of the wire remains constant, we have:
A⋅L=A′⋅L′
where A is the original cross-sectional area and A′ is the new cross-sectional area. Therefore:
A⋅L=A′⋅(2L)⟹A′=A2
The resistance R′ of the wire after stretching can be calculated using the formula:
R′=ρL′A′
Substituting L′=2L and A′=A2:
R′=ρ2LA2=ρ4LA
Since the original resistance R is given by:
R=ρLA=3Ω
we can substitute this into the equation for R′:
R′=4⋅R=4⋅3=12Ω
When the wire is bent to form a circular loop, the total length of the wire is equal to the circumference of the circle:
C=2πr=2L
From this, we can find the radius r:
r=Lπ
The angle subtended by points P and Q at the center is 60∘ or π3 radians. The length of the arc PQ can be calculated as:
Length of arc PQ=r⋅θ=r⋅π3=Lπ⋅π3=L3
The resistance R1 of the arc PQ is proportional to its length:
R1=R′⋅Length of arc PQC=12Ω⋅L32L=12Ω⋅16=2Ω
The remaining length of the wire (the rest of the loop) is:
Remaining length=2L−L3=6L3−L3=5L3
The resistance R2 of this remaining part is:
R2=R′⋅Remaining lengthC=12Ω⋅5L32L=12Ω⋅56=10Ω
The resistances R1 and R2 are in parallel:
1Req=1R1+1R2=12+110
Finding a common denominator (10):
1Req=510+110=610=35
Thus,
Req=53Ω
The equivalent resistance between points P and Q is:
53Ω
Topper's Solved these Questions
Similar Questions
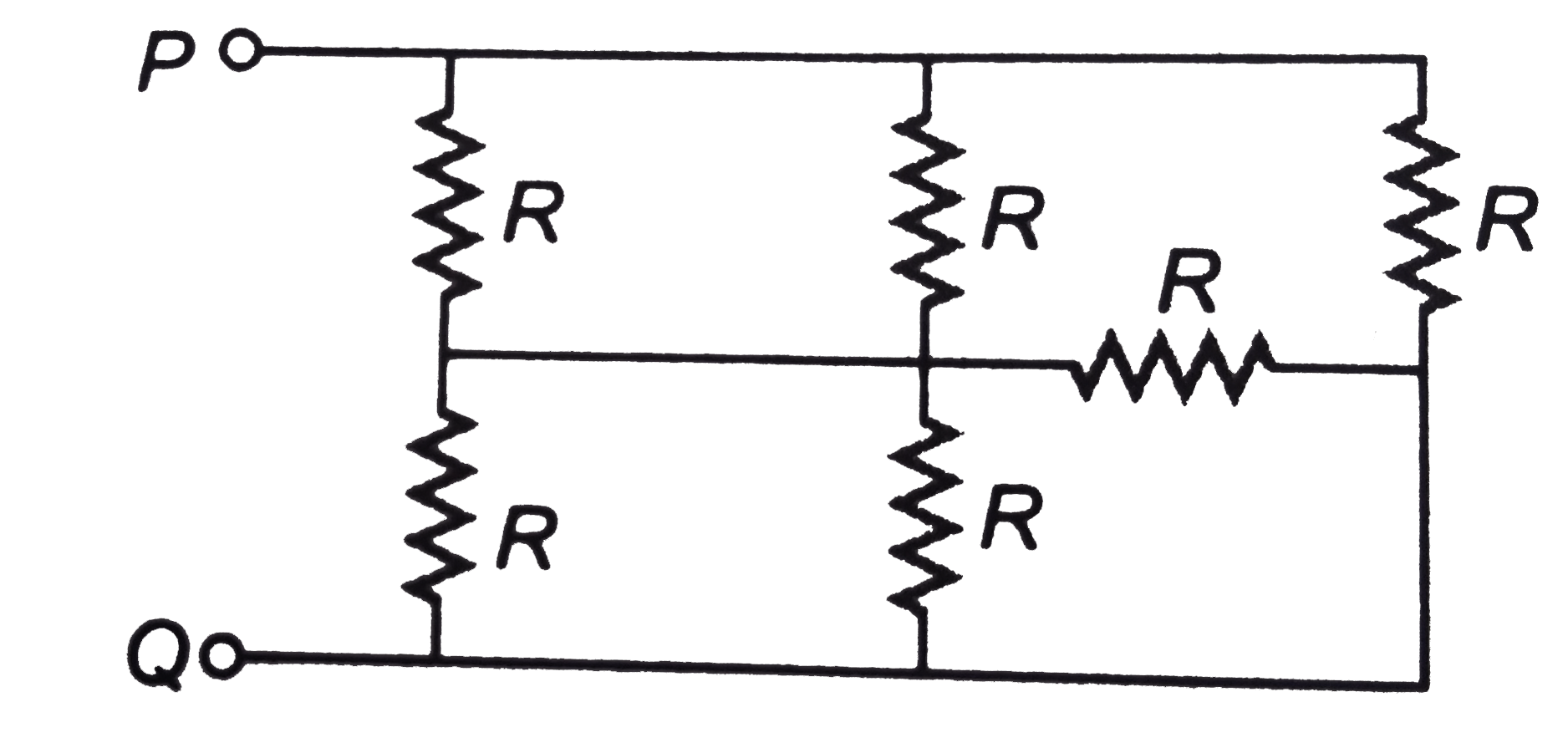
In the given figure, equivalent resistance between points P and Q is
View SolutionA given wire of resistance 1 Ω is stretched to double its length. What will be its new resistance ?
View SolutionIn the circuit shown in figure R=55Ω the equivalent resistance between the point P and Q is
View SolutionA metal wire of resistance 3ω is elongated to make a unform wire of double its previous length. This new wire is now bent and the ends joined to make a circle. If two points on this circle make an angle 60∘ at the centre, the equivalent resistance between these two points will be :
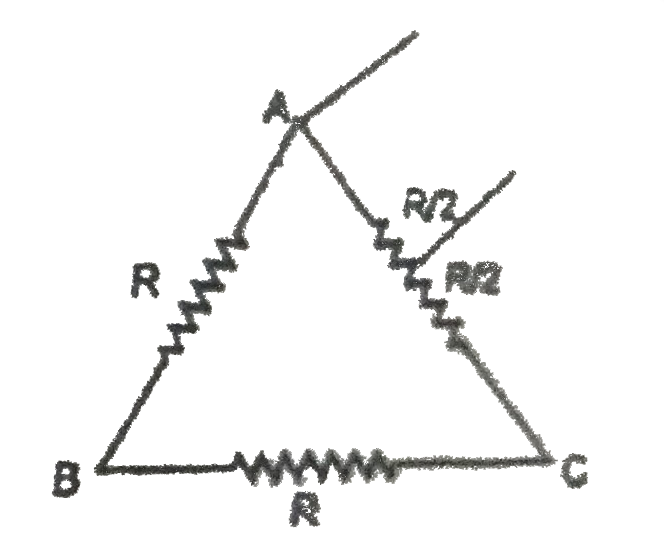
View SolutionA wire is bent in the form of a triangle now the equivalent resistance between its one end and the mid point of the side is
View SolutionA current I is flowing in a conductor of length L when it is bent in the form of a circular loop its magnetic moment
View SolutionA wire of resistance 3 ohm and length 10 cm is stretched to length 30 cm. Assuming that it has a uniform cross section, what will be its new resistance ?
View SolutionA uniform wire of resistance 9Ω is joined end-to-end to from a circle. Then, the resistance of the circular wire between any two diametrically points is
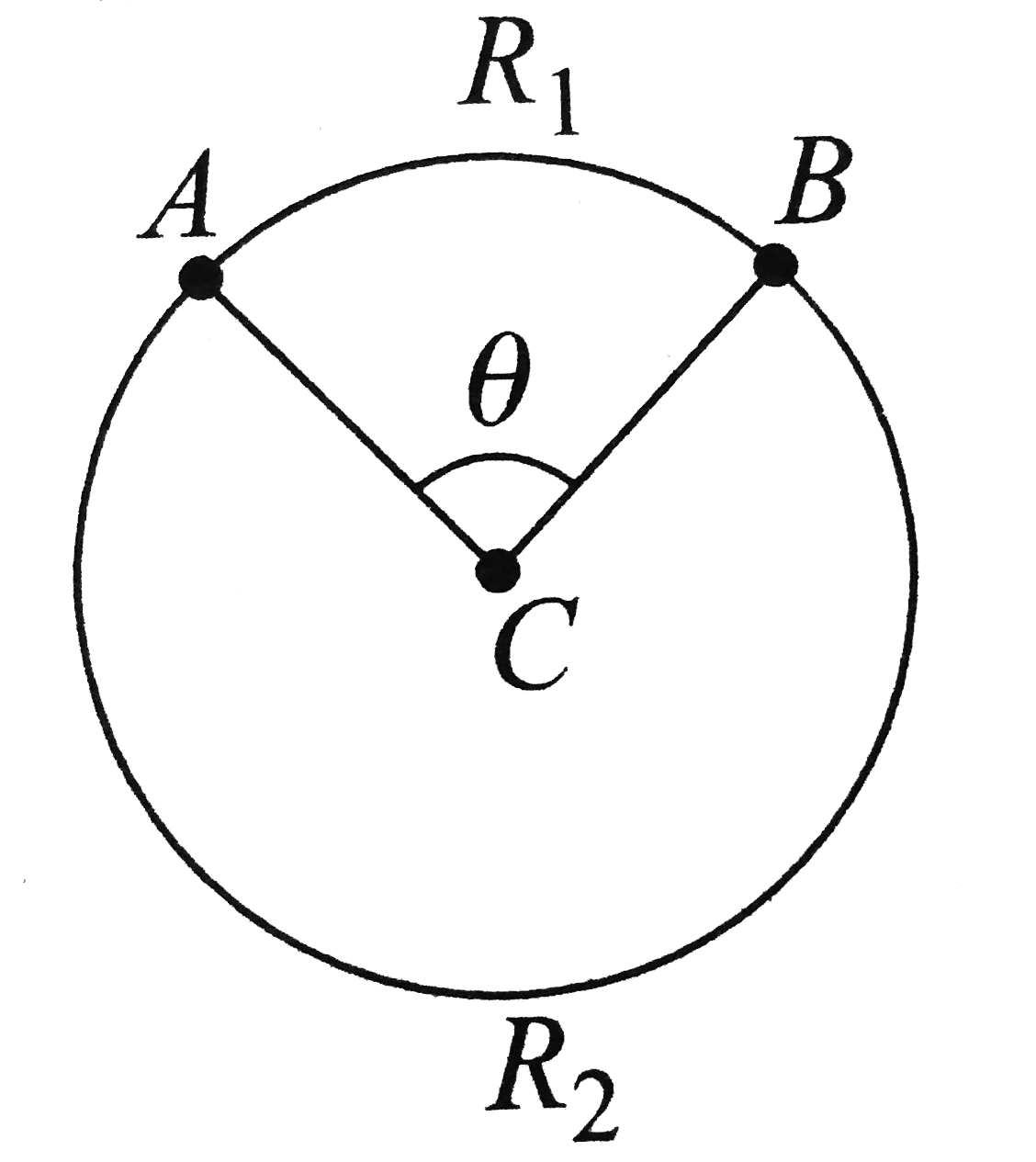
View SolutionIn a uniform ring of resistance R there are two points A and B such that ∠ACB=θ, where C is the centre of the ring. The equivalent resistance between A and B is
View SolutionA wire has resistance 12Ω. It is bent in the form of a circle. The effective resistance between two points across a diameter is.
View Solution

