In a ΔABC, altitude drawn from vertex A to side BC meets BC at D such that DB=3CD. Prove that 2AB2=2AC2+BC2
The correct Answer is:r2<p2+q2
To prove that 2AB2=2AC2+BC2 in triangle ΔABC where the altitude from vertex A to side BC meets BC at point D such that DB=3CD, we can follow these steps:
1. Define the segments on BC:
Let CD=x. Then, since DB=3CD, we have:
DB=3x
Therefore, the total length of BC is:
BC=BD+CD=3x+x=4x
2. Identify the lengths of BD and CD:
From the above, we can express:
BD=34BCandCD=14BC
3. Apply the Pythagorean theorem in triangles ABD and ACD:
In triangle ABD:
AB2=AD2+BD2
In triangle ACD:
AC2=AD2+CD2
4. Express AD2 in terms of AC2 and CD2:
Rearranging the equation for AC2:
AD2=AC2−CD2
Substitute CD=14BC:
CD2=(14BC)2=116BC2
Thus,
AD2=AC2−116BC2
5. Substitute AD2 into the equation for AB2:
Now substitute AD2 into the equation for AB2:
AB2=(AC2−116BC2)+BD2
Substitute BD=34BC:
BD2=(34BC)2=916BC2
Therefore,
AB2=AC2−116BC2+916BC2
Simplifying this gives:
AB2=AC2+816BC2=AC2+12BC2
6. Multiply the entire equation by 2:
To prove the required statement, multiply both sides by 2:
2AB2=2AC2+BC2
Conclusion:
Thus, we have proven that:
2AB2=2AC2+BC2
Let CD=x. Then, since DB=3CD, we have:
DB=3x
Therefore, the total length of BC is:
BC=BD+CD=3x+x=4x
From the above, we can express:
BD=34BCandCD=14BC
In triangle ABD:
AB2=AD2+BD2
In triangle ACD:
AC2=AD2+CD2
Rearranging the equation for AC2:
AD2=AC2−CD2
Substitute CD=14BC:
CD2=(14BC)2=116BC2
Thus,
AD2=AC2−116BC2
Now substitute AD2 into the equation for AB2:
AB2=(AC2−116BC2)+BD2
Substitute BD=34BC:
BD2=(34BC)2=916BC2
Therefore,
AB2=AC2−116BC2+916BC2
Simplifying this gives:
AB2=AC2+816BC2=AC2+12BC2
To prove the required statement, multiply both sides by 2:
2AB2=2AC2+BC2
Thus, we have proven that:
2AB2=2AC2+BC2
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5A47videos
CONGRUENCE AND SIMILAR TRIANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B8videos
CONGRUENCE AND SIMILAR TRIANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B27videos
CIRCLE AND ITS TANGENT LINES
- BOOK - LUCENT PUBLICATIONCHAPTER - ELEMENTARY TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE 11B37videos
ELEMENTARY TRIGONOMETRIC IDENTITIES
Similar Questions
The perpendicular from A on side BC of a ΔABC meets BC at D such that DB = 3CD .Prove that 2AB2=2AC2+BC2.
View SolutionThe perpendicular drawn from A on sides BC of a ΔABC intersects BC at D such that DB = 3CD .Prove that 2AB2=2AC2+BC2.
View SolutionIn the given figure, the of a ΔABC, interesects BC at D such DB=3CD. Prove that 2AB2=2AC2+BC2
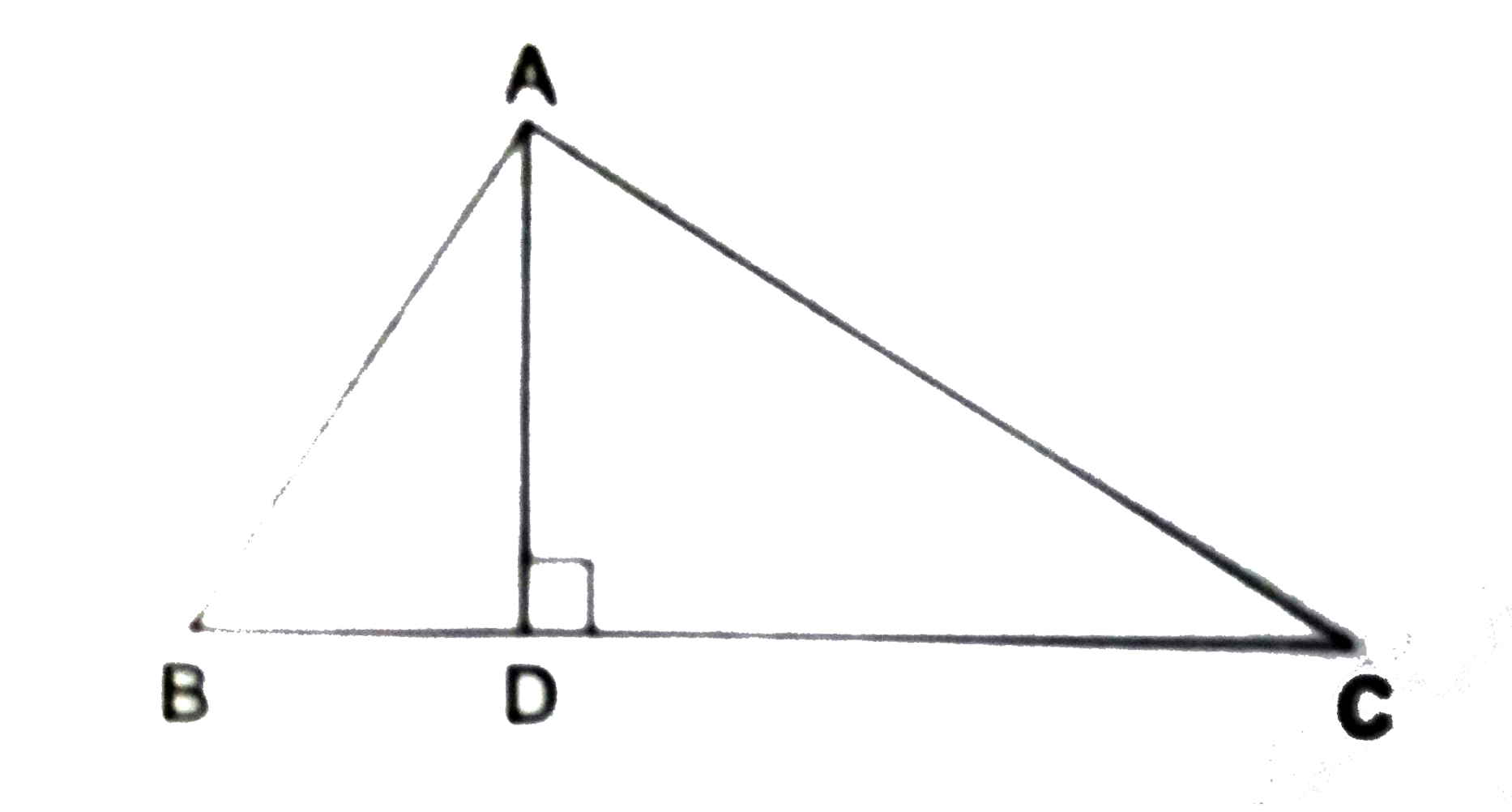 View Solution
View SolutionIn ΔABC, seg AD⊥ seg BCDB=3CD.
Prove that : 2AB2=2AC2+BC2
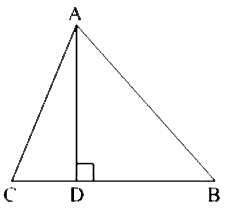 View Solution
View SolutionIn ΔABC seg AD⊥segBC,DB=3CD Prove that 2AB2=2AC2+BC2
View SolutionThe perpendicular from A on side BC of a ABC intersects BC at D such that DB = 3 CD. Prove that 2AB2=2AC2+BC2.
View SolutionThe perpendicular from A on side BC of a ΔABC meets BC at D such that DB = 3CD. Prove that 2AB2=2AC2+BC2
View SolutionIn ΔABC,
seg AD⊥ seg BC,
DB=3CD.
Prove that 2AB2=2AC2+BC2.
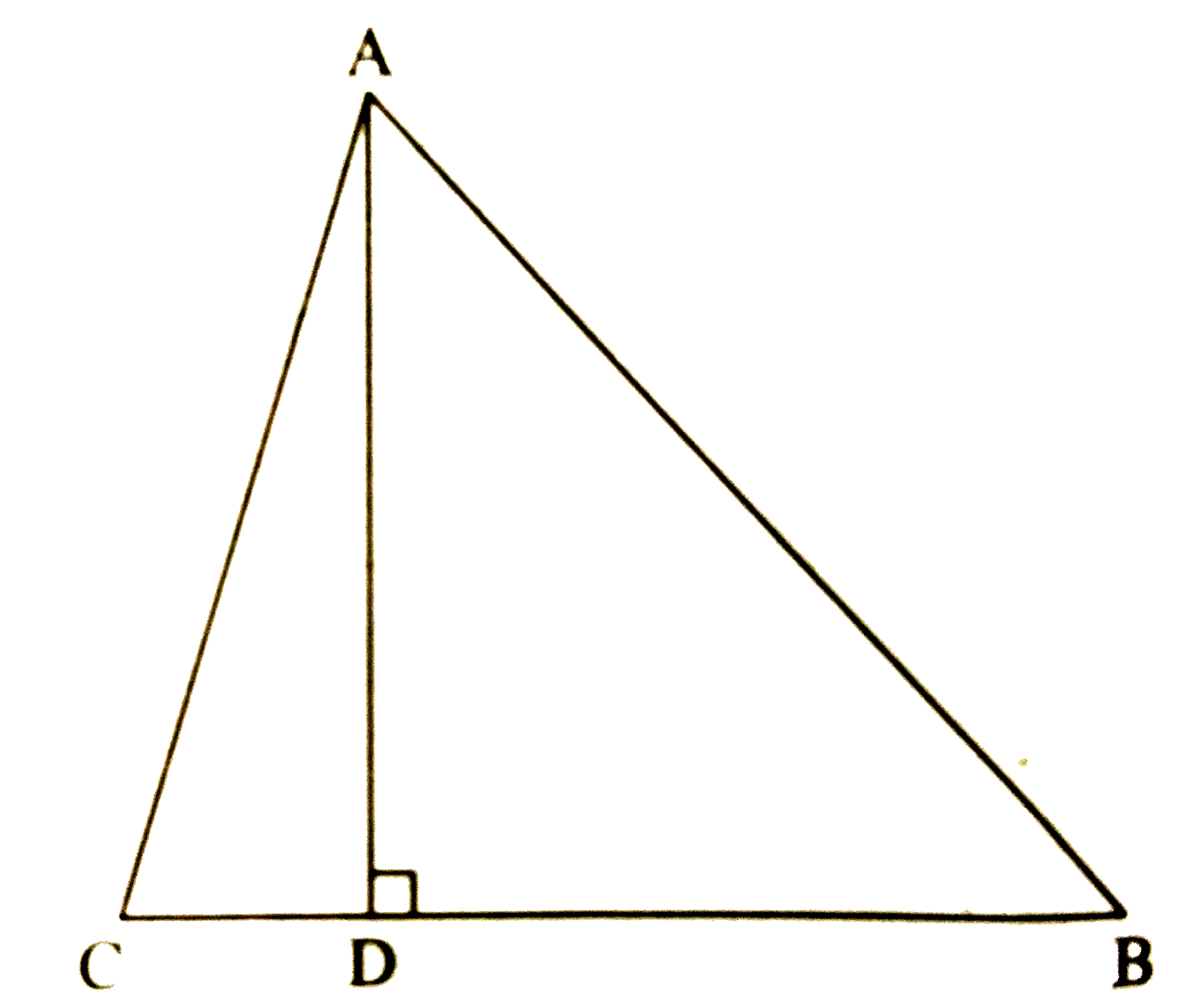 View Solution
View SolutionThe perpendicular AD on the base BC of a ABC intersects BC at D so that DB=3CD . Prove that 2 AB2=2 AC2+BC2 .
View SolutionThe perpendicular AD on the base BC of a △ABC intersects BC at D, so that DB=3CD. Prove that 2AB2=2AC2+BC2
View Solution

