The perpendicular drawn from A on sides BC of a intersects BC at D such that DB = 3CD .Prove that .
To prove that 2AB2=2AC2+BC2 given that the perpendicular from point A to side BC intersects at point D such that DB=3CD, we can follow these steps:
Step 1: Define the lengths
Let:
- CD=x
- Then, DB=3x
- Therefore, the total length BC=BD+CD=3x+x=4x
Step 2: Apply Pythagorean Theorem in triangle ABD
In triangle ABD, we can apply the Pythagorean theorem:
AB2=AD2+BD2
Substituting BD=3x:
AB2=AD2+(3x)2
AB2=AD2+9x2(1)
Step 3: Apply Pythagorean Theorem in triangle ACD
In triangle ACD, we apply the Pythagorean theorem:
AC2=AD2+CD2
Substituting CD=x:
AC2=AD2+x2(2)
Step 4: Subtract equation (2) from equation (1)
Now, we subtract equation (2) from equation (1):
AB2−AC2=(AD2+9x2)−(AD2+x2)
This simplifies to:
AB2−AC2=9x2−x2
AB2−AC2=8x2(3)
Step 5: Express BC2 in terms of x
Now, we can express BC2:
BC=4x⟹BC2=(4x)2=16x2(4)
Step 6: Relate AB2 and AC2 to BC2
From equation (3), we can express AB2 in terms of AC2 and x:
AB2=AC2+8x2
Now, we can multiply both sides by 2:
2AB2=2AC2+16x2(5)
Step 7: Substitute 16x2 from equation (4)
Now, substitute 16x2 from equation (4) into equation (5):
2AB2=2AC2+BC2
Conclusion
Thus, we have proved that:
2AB2=2AC2+BC2
Let:
- CD=x
- Then, DB=3x
- Therefore, the total length BC=BD+CD=3x+x=4x
In triangle ABD, we can apply the Pythagorean theorem:
AB2=AD2+BD2
Substituting BD=3x:
AB2=AD2+(3x)2
AB2=AD2+9x2(1)
In triangle ACD, we apply the Pythagorean theorem:
AC2=AD2+CD2
Substituting CD=x:
AC2=AD2+x2(2)
Now, we subtract equation (2) from equation (1):
AB2−AC2=(AD2+9x2)−(AD2+x2)
This simplifies to:
AB2−AC2=9x2−x2
AB2−AC2=8x2(3)
Now, we can express BC2:
BC=4x⟹BC2=(4x)2=16x2(4)
From equation (3), we can express AB2 in terms of AC2 and x:
AB2=AC2+8x2
Now, we can multiply both sides by 2:
2AB2=2AC2+16x2(5)
Now, substitute 16x2 from equation (4) into equation (5):
2AB2=2AC2+BC2
Thus, we have proved that:
2AB2=2AC2+BC2
Topper's Solved these Questions
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Triangles) (Multiple Choice Questions)
8 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Triangles) (Very Short Answer type Questions )
17 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -III: Coordinate Geometry (Coordinate Geometry ) (Very Short Answer Type Questions )
13 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
Similar Questions
The perpendicular from A on side BC of a ΔABC meets BC at D such that DB = 3CD .Prove that 2AB2=2AC2+BC2.
View SolutionThe perpendicular from A on side BC of a ABC intersects BC at D such that DB = 3 CD. Prove that 2AB2=2AC2+BC2.
View SolutionThe perpendicular from A on side BC of a ΔABC meets BC at D such that DB = 3CD. Prove that 2AB2=2AC2+BC2
View SolutionIn the given figure, the of a ΔABC, interesects BC at D such DB=3CD. Prove that 2AB2=2AC2+BC2
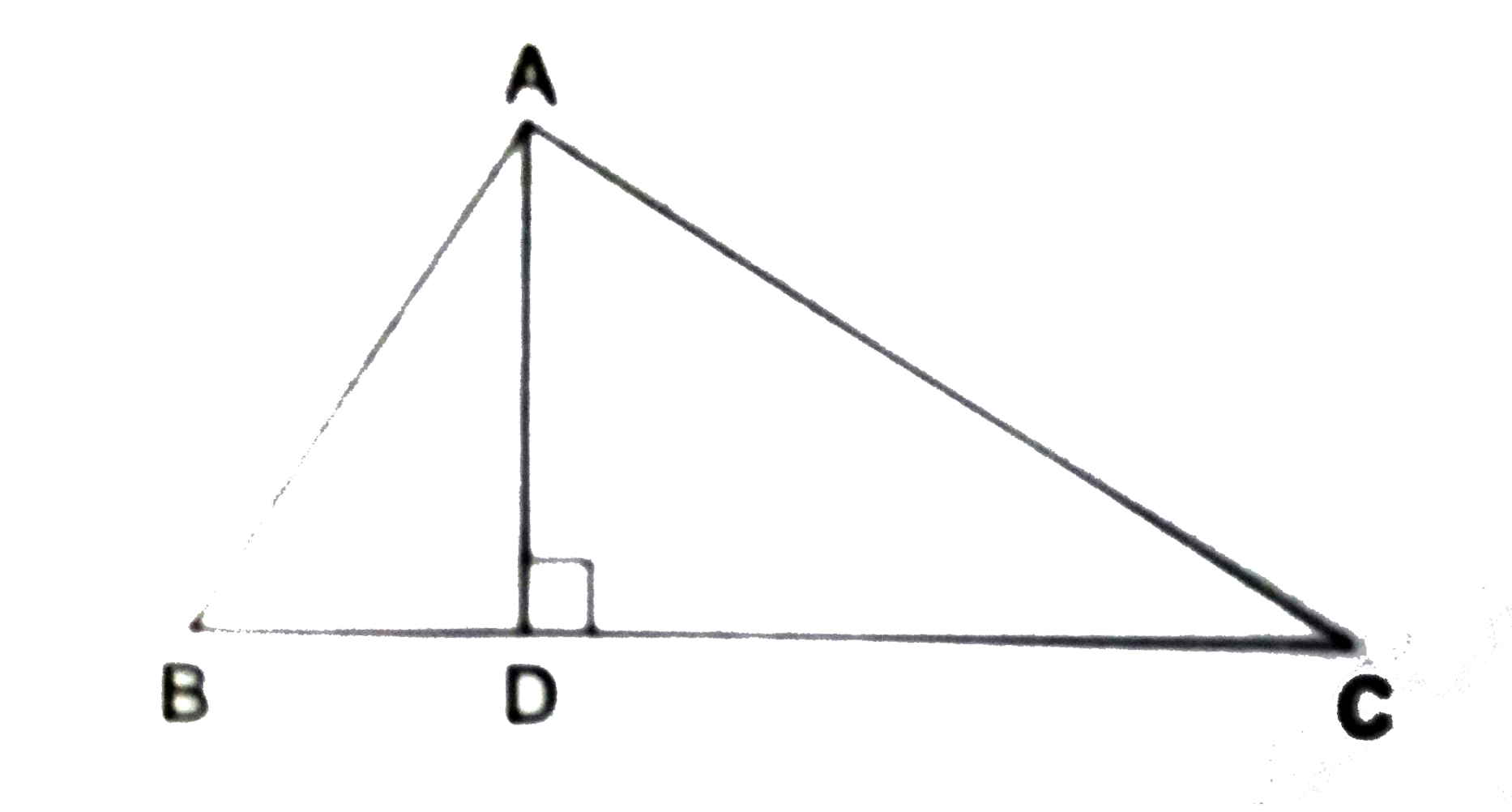
View SolutionThe perpendicular AD on the base BC of a ABC intersects BC at D so that DB=3CD . Prove that 2 AB2=2 AC2+BC2 .
View SolutionThe perpendicular AD on the base BC of a △ABC intersects BC at D, so that DB=3CD. Prove that 2AB2=2AC2+BC2
View SolutionIn a ΔABC, altitude drawn from vertex A to side BC meets BC at D such that DB=3CD. Prove that 2AB2=2AC2+BC2
View SolutionIn ΔABC seg AD⊥segBC,DB=3CD Prove that 2AB2=2AC2+BC2
View SolutionIn ΔABC, seg AD⊥ seg BCDB=3CD.
Prove that : 2AB2=2AC2+BC2
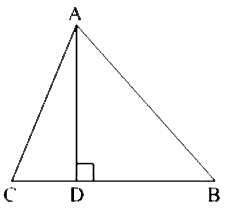
View SolutionIn ΔABC,
seg AD⊥ seg BC,
DB=3CD.
Prove that 2AB2=2AC2+BC2.
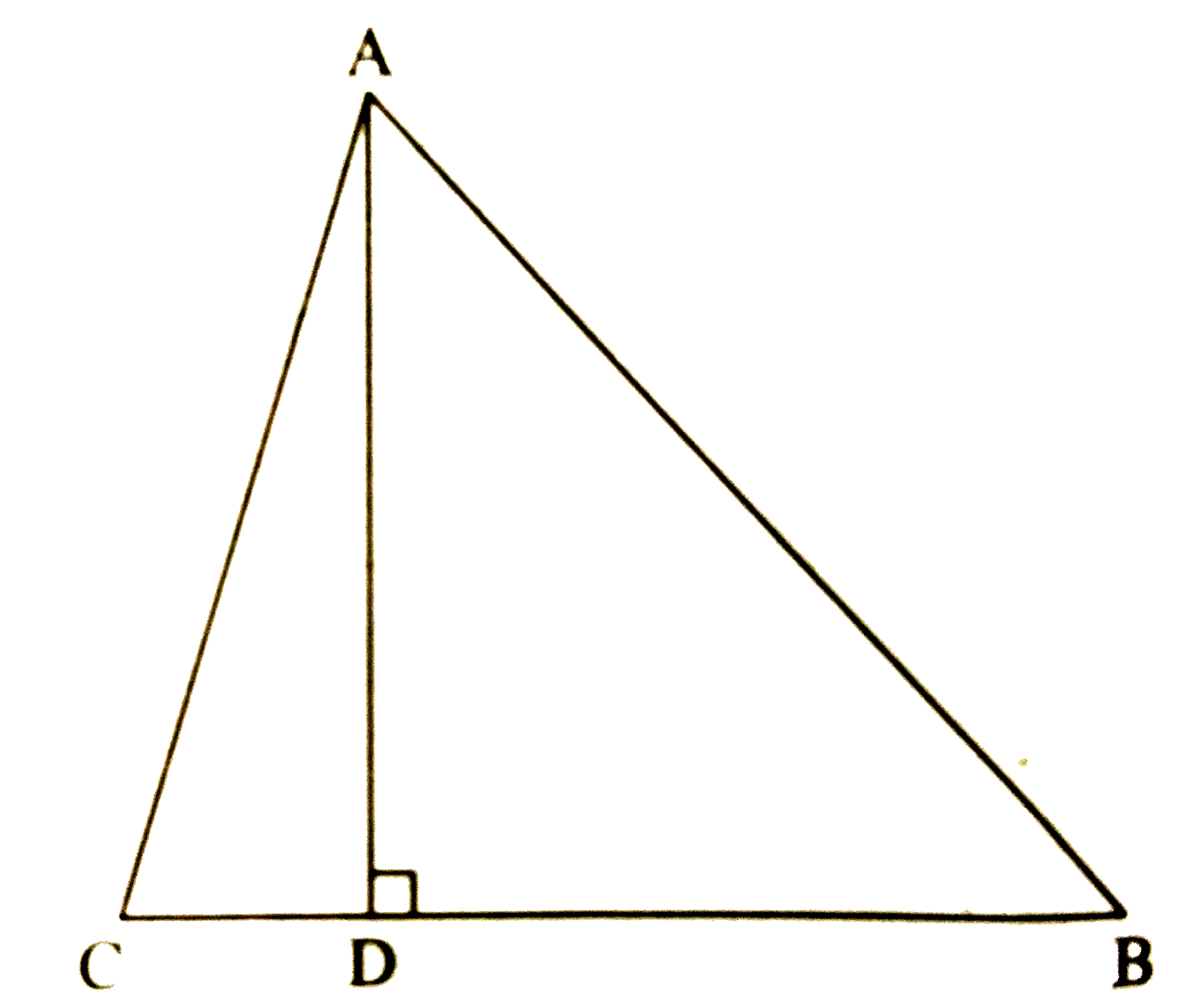
View Solution
