A spherical shell of mass 50kg and radius 50m. A mass of 15kg is kept at center. Find value of gravitational potential at a distance 25m from center.
To find the gravitational potential at a distance of 25 meters from the center of a spherical shell with a mass of 50 kg and a mass of 15 kg at the center, we can follow these steps:
1. Understanding Gravitational Potential:
The gravitational potential V at a distance r from a mass M is given by the formula:
V=−GMr
where G is the gravitational constant.
2. Identify the Components:
- The spherical shell has a mass Ms=50kg and radius R=50m.
- The mass at the center is Mc=15kg.
- We need to find the gravitational potential at a distance r=25m from the center.
3. Potential Due to the Spherical Shell:
According to the shell theorem, the gravitational potential outside a spherical shell is the same as if all the mass were concentrated at the center. However, inside the shell, the potential is constant and equal to the potential at the surface of the shell. Since 25 m is less than the radius of the shell (50 m), we need to calculate the potential due to the shell at the surface:
Vs=−GMsR=−G⋅5050=−G
4. Potential Due to the Mass at the Center:
The potential due to the mass at the center at a distance of 25 m is:
Vc=−GMcr=−G⋅1525=−3G5
5. Total Gravitational Potential:
The total gravitational potential V at a distance of 25 m from the center is the sum of the potentials due to the shell and the mass at the center:
V=Vs+Vc=−G−3G5
To combine these, convert −G to a common denominator:
V=−5G5−3G5=−8G5
Final Answer:
Thus, the gravitational potential at a distance of 25 m from the center is:
V=−8G5
The gravitational potential V at a distance r from a mass M is given by the formula:
V=−GMr
where G is the gravitational constant.
- The spherical shell has a mass Ms=50kg and radius R=50m.
- The mass at the center is Mc=15kg.
- We need to find the gravitational potential at a distance r=25m from the center.
According to the shell theorem, the gravitational potential outside a spherical shell is the same as if all the mass were concentrated at the center. However, inside the shell, the potential is constant and equal to the potential at the surface of the shell. Since 25 m is less than the radius of the shell (50 m), we need to calculate the potential due to the shell at the surface:
Vs=−GMsR=−G⋅5050=−G
The potential due to the mass at the center at a distance of 25 m is:
Vc=−GMcr=−G⋅1525=−3G5
The total gravitational potential V at a distance of 25 m from the center is the sum of the potentials due to the shell and the mass at the center:
V=Vs+Vc=−G−3G5
To combine these, convert −G to a common denominator:
V=−5G5−3G5=−8G5
Thus, the gravitational potential at a distance of 25 m from the center is:
V=−8G5
Similar Questions
A shell has mass 100 kg and radius 50m. A point mass 50 kg is placed at center of shell. Find potential at a pont 25m from center of shell.

View SolutionA particle of mass M is placed at the centre of a spherical shell of same mass and radius a. What will be the magnitude of the gravitational potential at a point situated at a/2 distance from the centre ?
View Solution
Knowledge Check
A particle of mass M is situated at the centre of a spherical shell of same mass and radius 'a'. The gravitational potential at a point situated at a2 distance from the centre, will be
A−3GMaB−2GMaC−GMaD−4GMaA shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
A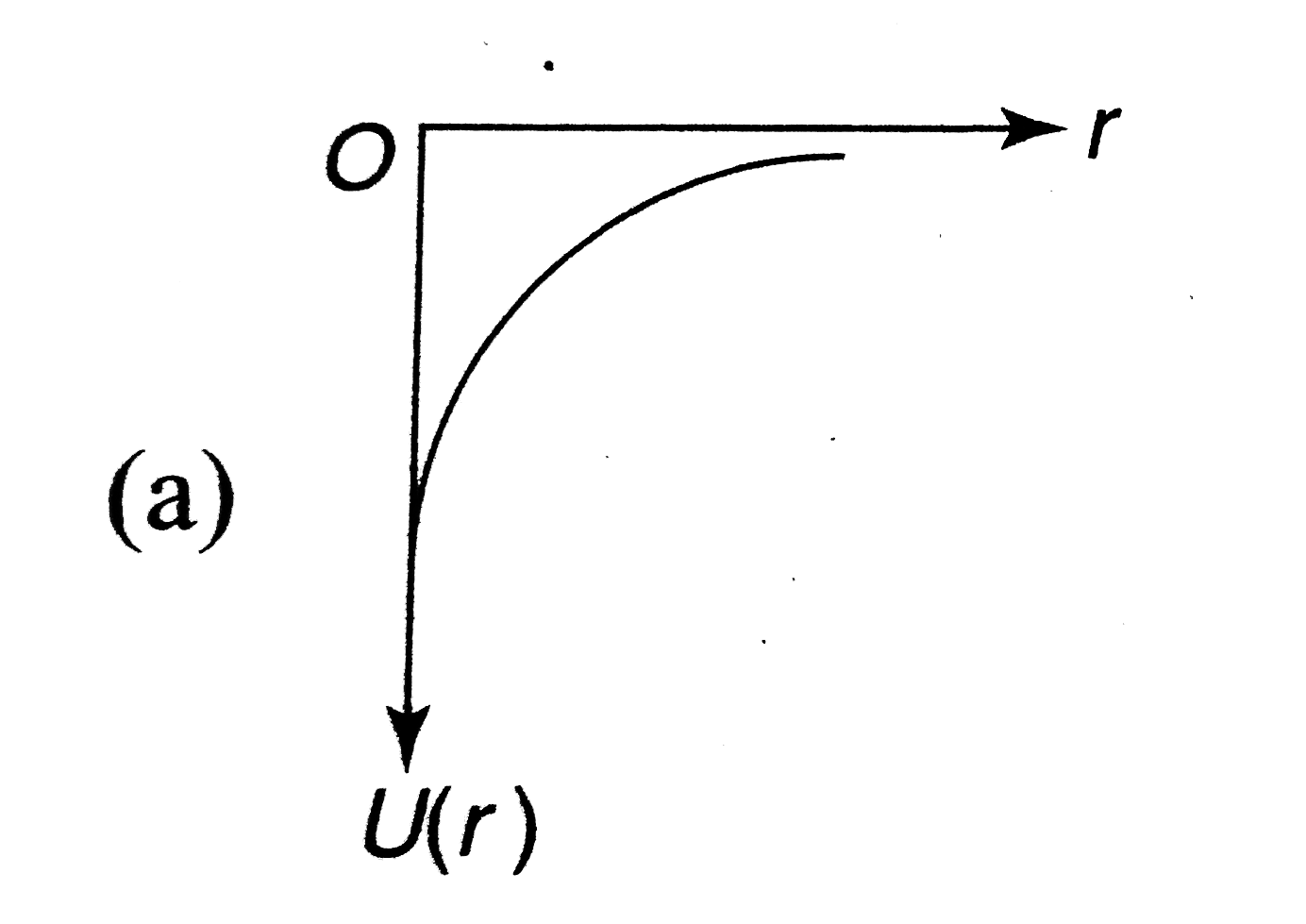 B
B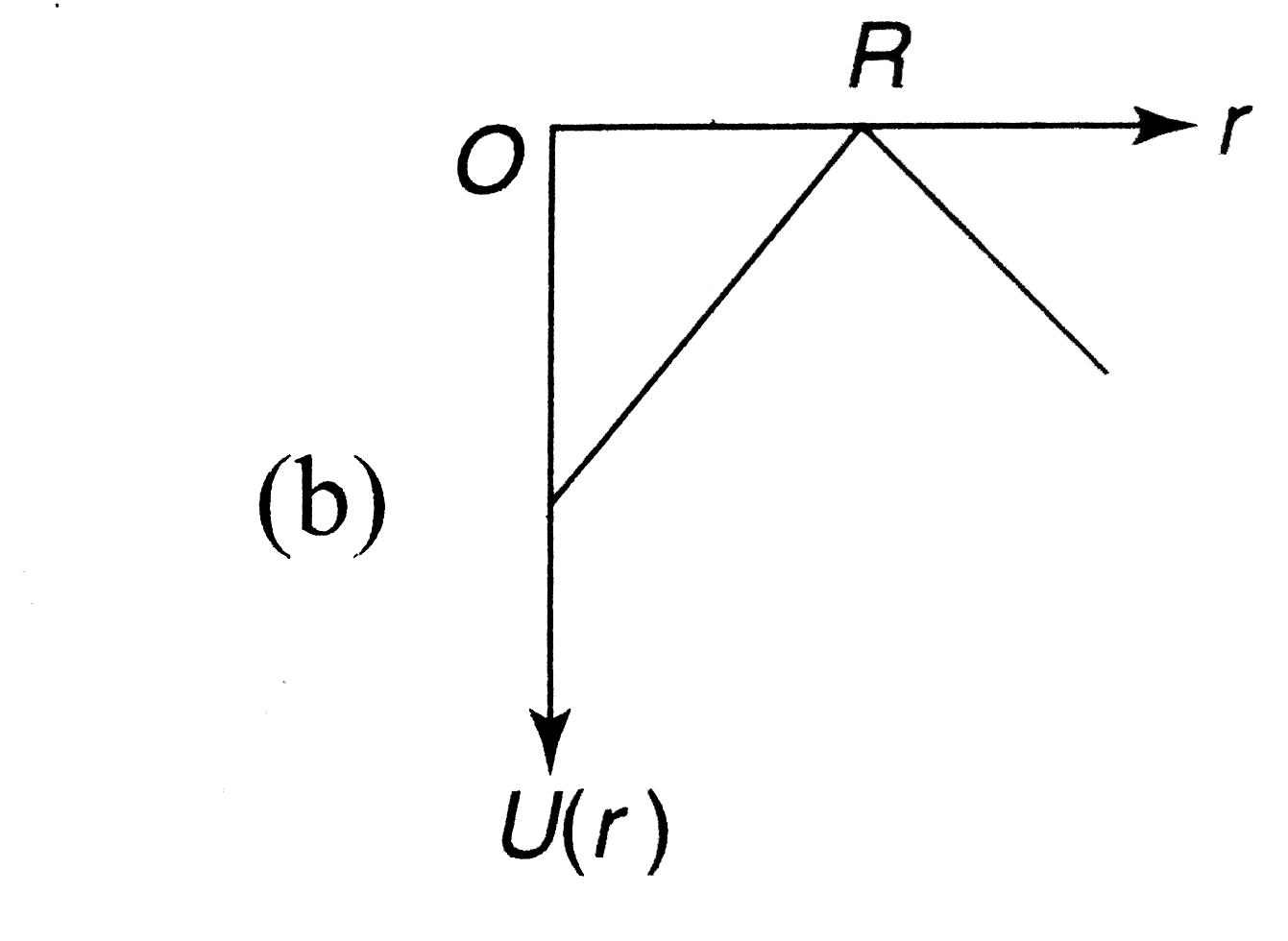 C
C D
D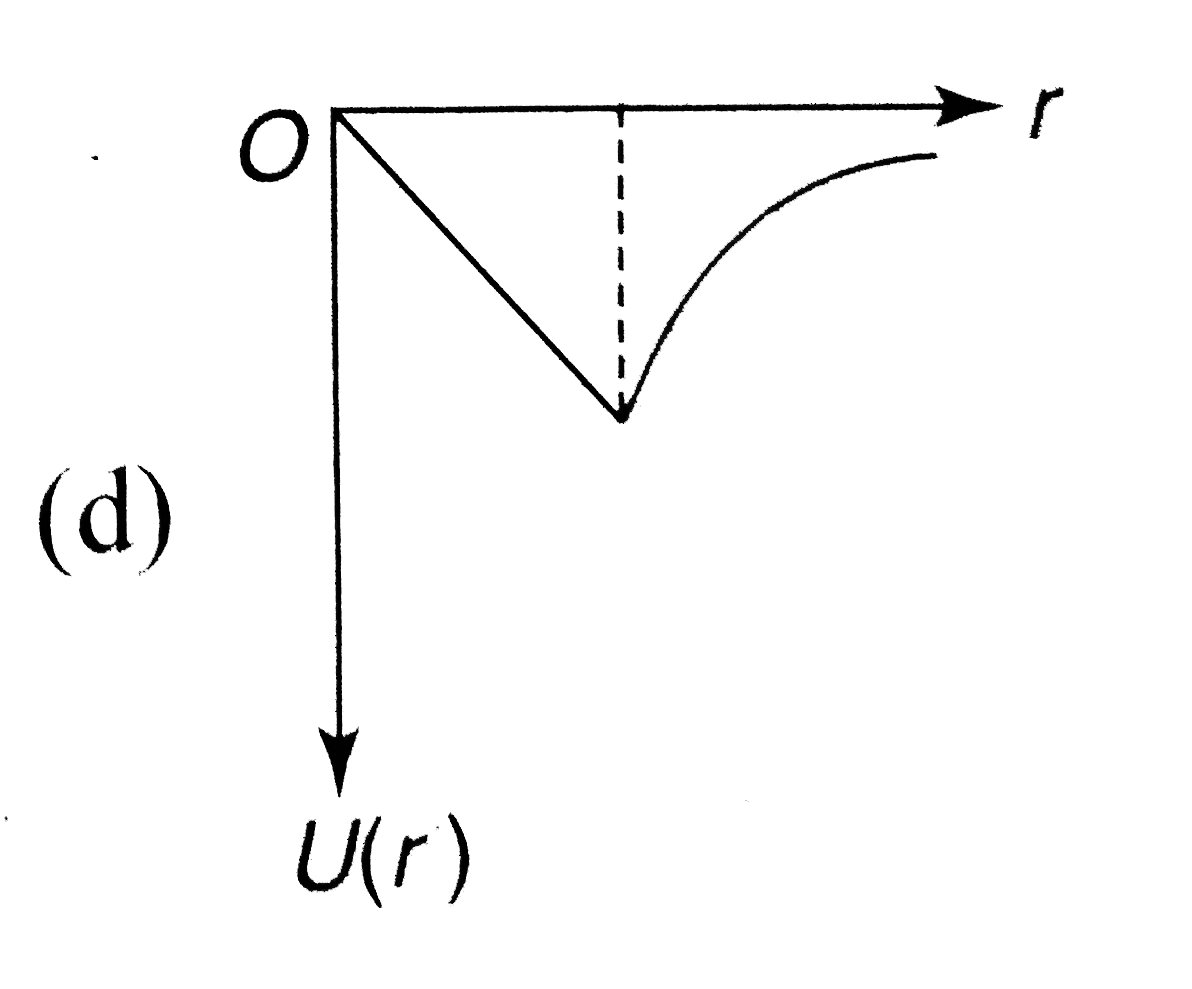
The M.I. of a wheel of mass 8 kg and radius of gyration 25 cm is
A5kgm2B1.5kgm2C2.5kgm2D0.5kgm2
A mass of 50 kg is placed at the centre of a uniform spherical shell of mass 100 kg and radius 50 m. If the gravitational potential at a point, 25 m from the centre is V kg/m. The value of V is:
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass 1 kg is kept on the surface of a uniform thin spherical shell of mass 20 kg and radius 1 m. Find the work to be done against the gravitational force between them to take the particle away from the thin spherical shell.
View SolutionFor a given uniform spherical shell of mass M and radius R find gravitational field at a distancer r from centre in following two cases (a) r≥R (b) r<R .
View SolutionA particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View Solution
