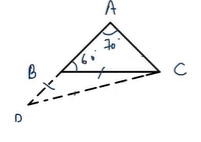
The side AC of a triangle ABC is produced to D such that BC=CD. If ∠ACB is 70∘, then what is ∠ADB equal to ?
35∘
45∘
70∘
110∘
To solve the problem, we need to find the measure of angle ADB in triangle ABC, where side AC is extended to point D such that BC = CD and angle ACB is given as 70 degrees.
1. Understand the Triangle Configuration:
We have triangle ABC with angle ACB = 70°. The side AC is extended to point D such that BC = CD.
2. Identify Angles:
Since BC = CD, triangle BCD is isosceles. Therefore, the angles opposite to the equal sides (BC and CD) are equal. Let's denote angle DBC as X and angle DCB as X.
3. Use the Exterior Angle Theorem:
The exterior angle ADB (which is the angle we want to find) is equal to the sum of the two opposite interior angles (angle ACB and angle DBC).
Therefore, we can write:
∠ADB=∠ACB+∠DBC
Since we have established that angle ACB = 70° and angle DBC = X, we can express this as:
∠ADB=70°+X
4. Calculate Angle DBC:
In triangle BCD, the sum of angles must equal 180°. Therefore, we can write:
∠DBC+∠DCB+∠BCD=180°
Substituting the known angles:
X+X+70°=180°
Simplifying gives:
2X+70°=180°
2X=180°−70°
2X=110°
X=55°
5. Find Angle ADB:
Now substituting back to find angle ADB:
∠ADB=70°+55°=125°
Final Answer:
Thus, the measure of angle ADB is 125 degrees.
We have triangle ABC with angle ACB = 70°. The side AC is extended to point D such that BC = CD.
Since BC = CD, triangle BCD is isosceles. Therefore, the angles opposite to the equal sides (BC and CD) are equal. Let's denote angle DBC as X and angle DCB as X.
The exterior angle ADB (which is the angle we want to find) is equal to the sum of the two opposite interior angles (angle ACB and angle DBC).
Therefore, we can write:
∠ADB=∠ACB+∠DBC
Since we have established that angle ACB = 70° and angle DBC = X, we can express this as:
∠ADB=70°+X
In triangle BCD, the sum of angles must equal 180°. Therefore, we can write:
∠DBC+∠DCB+∠BCD=180°
Substituting the known angles:
X+X+70°=180°
Simplifying gives:
2X+70°=180°
2X=180°−70°
2X=110°
X=55°
Now substituting back to find angle ADB:
∠ADB=70°+55°=125°
Thus, the measure of angle ADB is 125 degrees.
Similar Questions
Knowledge Check
The side AC of a ΔABC is extended to D such that BC = CD. If ∠ACB is 70∘ ,then what is ∠ADB equal to ?
A35∘B45∘C70∘D110∘ABC is an isosceles triangle with AB = AC. Side BA is produced to D such that AB=AD. Find the ∠BCD:
A45∘B90∘C30∘D60∘In the given figure, side BC of ∠ABC is produced to D such that ∠ABC=70∘ and ∠ACD=120∘. Then, ∠ BAC = ?
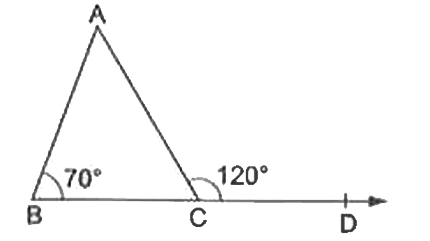 A60∘B50∘C70∘D35∘
A60∘B50∘C70∘D35∘
In a triangle ABC, ∠ABC=45∘ and a point D is on BC such that 2BD=CD and ∠DAB=15∘ then ∠ACB=
View SolutionLet ABC be an equilateral triangle. If the side BC is produced to the point D so that BC = 2CD, then AD2 is equal to
View SolutionIn a ΔABC, BC is produced to D such that CD=AC is ∠BAD=111∘,∠ACB=80∘. Find ∠ABC=?
View SolutionABC is a equilateral triangle and CD is internal bisector of ∠C. If DC is extended to E in such a way that AC = CE then ∠CAE is-
View SolutionIn the figure shown here, a circle touches the side BC of a triangle ABC at P and AB and AC produced at Q and R respectively. What is AQ equal to ?
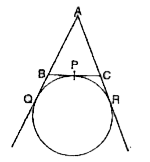
View Solution