A cylinder is surmounted by a cone at one end, a hemisphere at the other end. The common radius is 3.5 cm, the height of the cylinder is 6.5 cm and the total height of the structure is 12.8 cm. The volume V of the structure lies between
370cm3and380cm2
380cm2and390cm3
390cm3and400cm3
None of the above
To find the volume of the structure composed of a cylinder, a cone, and a hemisphere, we will follow these steps:
Step 1: Identify the dimensions
- Common radius (r) = 3.5 cm
- Height of the cylinder (h_cylinder) = 6.5 cm
- Total height of the structure = 12.8 cm
Step 2: Calculate the height of the cone
The total height of the structure is the sum of the heights of the cylinder, cone, and hemisphere. The height of the hemisphere is equal to its radius.
Let the height of the cone be hcone.
- Height of the hemisphere = radius = 3.5 cm
Using the total height:
hcylinder+hcone+hhemisphere=12.8
Substituting the known values:
6.5+hcone+3.5=12.8
hcone=12.8−6.5−3.5=2.8 cm
Step 3: Calculate the volume of the cylinder
The formula for the volume of a cylinder is:
Vcylinder=πr2hcylinder
Substituting the values:
Vcylinder=π(3.5)2(6.5)=π(12.25)(6.5)=79.625π cm3
Step 4: Calculate the volume of the cone
The formula for the volume of a cone is:
Vcone=13πr2hcone
Substituting the values:
Vcone=13π(3.5)2(2.8)=13π(12.25)(2.8)=34.33π cm3
Step 5: Calculate the volume of the hemisphere
The formula for the volume of a hemisphere is:
Vhemisphere=23πr3
Substituting the values:
Vhemisphere=23π(3.5)3=23π(42.875)=28.5833π cm3
Step 6: Calculate the total volume
Now, we will add the volumes of all three parts:
Vtotal=Vcylinder+Vcone+Vhemisphere
Substituting the calculated volumes:
Vtotal=79.625π+34.33π+28.5833π
To simplify, we can find a common denominator for the cone's volume:
34.33=11.4333π
Thus,
Vtotal=(79.625+11.4333+28.5833)π=119.6416π cm3
Step 7: Calculate the numerical value
Using π≈3.14:
Vtotal≈119.6416×3.14≈375.76 cm3
Conclusion
The total volume of the structure lies between 370 cm³ and 380 cm³.
---
- Common radius (r) = 3.5 cm
- Height of the cylinder (h_cylinder) = 6.5 cm
- Total height of the structure = 12.8 cm
The total height of the structure is the sum of the heights of the cylinder, cone, and hemisphere. The height of the hemisphere is equal to its radius.
- Height of the hemisphere = radius = 3.5 cm
hcylinder+hcone+hhemisphere=12.8
Substituting the known values:
6.5+hcone+3.5=12.8
hcone=12.8−6.5−3.5=2.8 cm
The formula for the volume of a cylinder is:
Vcylinder=πr2hcylinder
Substituting the values:
Vcylinder=π(3.5)2(6.5)=π(12.25)(6.5)=79.625π cm3
The formula for the volume of a cone is:
Vcone=13πr2hcone
Substituting the values:
Vcone=13π(3.5)2(2.8)=13π(12.25)(2.8)=34.33π cm3
The formula for the volume of a hemisphere is:
Vhemisphere=23πr3
Substituting the values:
Vhemisphere=23π(3.5)3=23π(42.875)=28.5833π cm3
Now, we will add the volumes of all three parts:
Vtotal=Vcylinder+Vcone+Vhemisphere
Substituting the calculated volumes:
Vtotal=79.625π+34.33π+28.5833π
To simplify, we can find a common denominator for the cone's volume:
34.33=11.4333π
Thus,
Vtotal=(79.625+11.4333+28.5833)π=119.6416π cm3
Using π≈3.14:
Vtotal≈119.6416×3.14≈375.76 cm3
The total volume of the structure lies between 370 cm³ and 380 cm³.
Similar Questions
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other end. Given that common radius =3.5 cm the height of the cylinder =6.5 cm and the total height =12.8 cm , claculate the volume of the solid correct to the nearest cm.
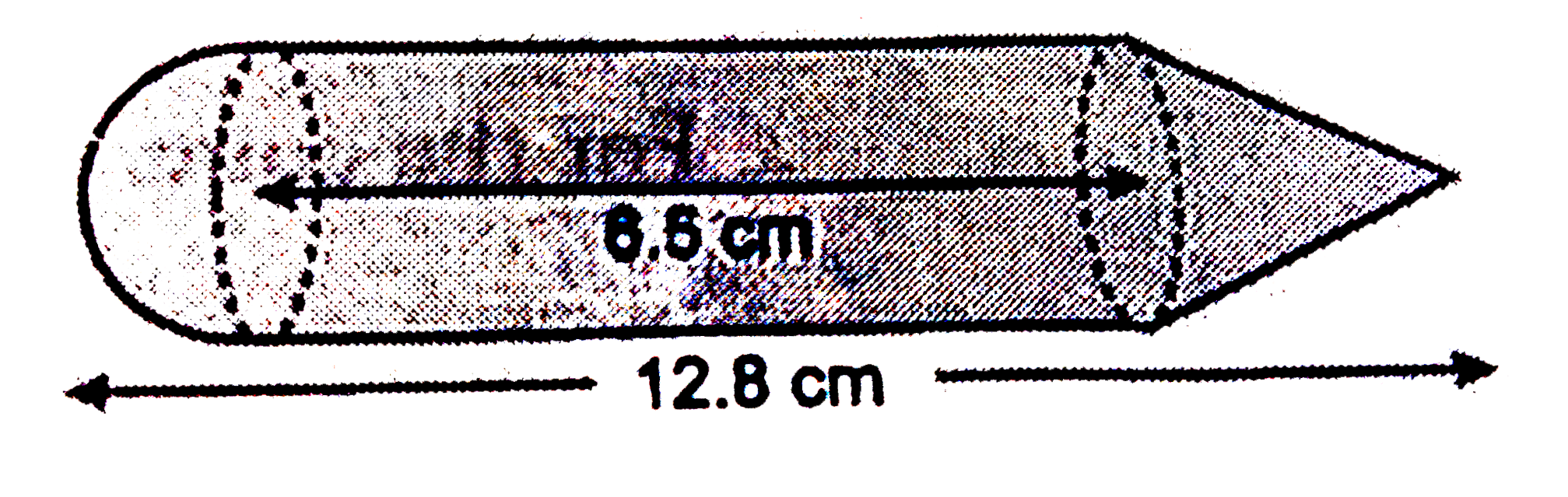
View SolutionThe material of a cone is covered into the shape of a cylinder of equal radius. If the height of the cylinder is 5 cm. then height of the cone is ___.
View Solution
Knowledge Check
The material of a cone is covered into the shape of a cylinder of equal radius. If the height of the cylinder is 5 cm. then height of the cone is ___.
A10 cmB15 cmC18 cmD24 cmA cone was melted and cast into a cylinder of the same radius as that of the base of the cone. If the height of the cylinder is 5cm, find the height of the cone.
A15 cmB10 cmC18 cmD5 cmA cone was melted and cast into a cylinder of the same radius as that of the base of the cone. If the height of the cylinder is 5 cm, then what is the height of the cone?
A15 cmB10 cmC18 cmD5 cm
The material of a cone is covered into the shape of a cylinder of equal radius. If the height of the cylinder is 5 cm. then height of the cone is ___.
View SolutionThe volume of a cylinder is 3850cubic cm.Find the height if the radius is 7cm
View SolutionThe material of a cone is covered into the shape of a cylinder of equal radius. If the height of the cylinder is 8 cm. then height of the cone is ___.
View SolutionThe material of a cone is covered into the shape of a cylinder of equal radius. If the height of the cylinder is 10 cm. then height of the cone is ___.
View SolutionThe following figure shows a model of rocket consisting of a cylinder surmounted by a cone at one end . The dimensions of the model are radius = 3 cm and height of the cone =4 cm and total height =14 cm. Find the (i) total surface area of the model in πm2 (ii) the total volume of model in πm3.

View Solution
