ABCD is a parallelogram and E is a point, on BC. If the diagonal BD intersects AE at F, prove that AF×FB×EF×FD.
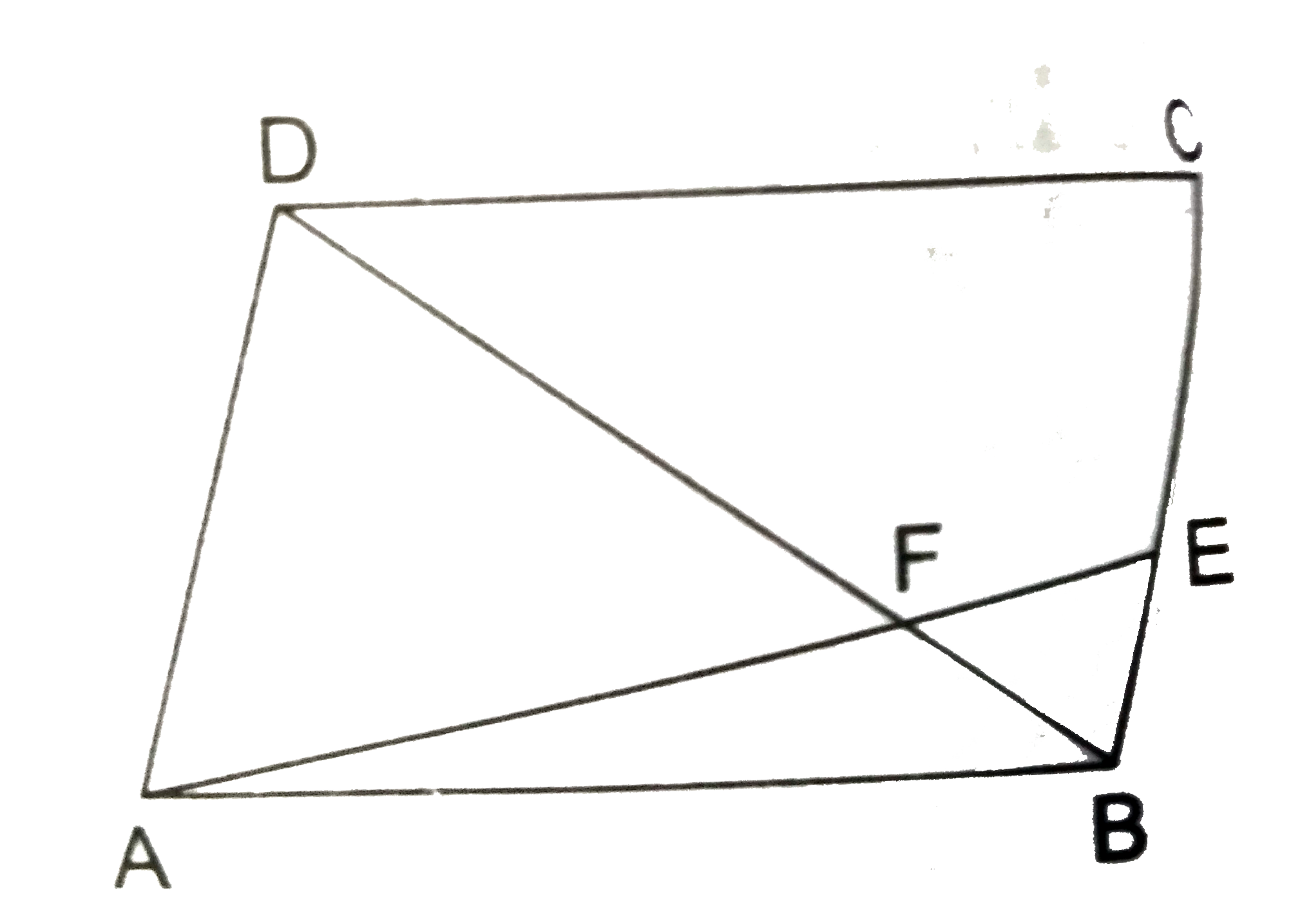
ΔAFD~ΔEFB,as∠AFD=∠EFB (vert. opp. ∠) and ∠DAF=∠BEF( alt. ∠)
∴AFEF=FDFB
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C13videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7D22videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7A12videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point P divides AL in the ratioA1:2B1:3C3:1D2:1 - Question 2 - Select One
ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point Q divides DB in the ratioA1:2B1:3C3:1D2:1
ABCD is a parallelogram. E is a point on BA such that BE=2EA and F is a point on Do such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third area of parallelogram AB CD
View SolutionABCD is a parallelogram. E is a point on BC such that BE : EC = m:n. If AE and DB intersect in F, then what is the ratio of the area of triangle FEB to the area of triangle AFD?
View SolutionABCD is a parallelogram. The circle through A,BandC intersects CD produced at E, prove that AE=AD.
View SolutionFind the angle between line x+12=y3=z−36 and the plane 10x+2y−11z−3=0.
View SolutionABCD is a parallelogram. E; F are mid point of BC; CD respectively. AE; AF meet the diagonal BD at points Q and P respectively. Show that points P and Q trisect DB.
View SolutionIn the given figure, ABCD is a parallelogram in which DC is extended to F such that AF intersects BC at E . Then perimeter of ΔABE=
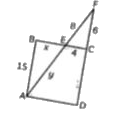 View Solution
View Solution


