When a ball bounces, it rises to of the height from which it fell. If the ball is dropped from a height of 36 m, how high will it rise at the third bounce?
m
To find out how high the ball will rise at the third bounce, we can follow these steps:
1. Initial Height: The ball is dropped from a height of 36 meters.
2. First Bounce: The ball rises to 23 of the height from which it fell. So, we calculate the height after the first bounce:
Height after first bounce=23×36=24 meters
3. Second Bounce: Now, we calculate the height after the second bounce, which is 23 of the height it reached after the first bounce:
Height after second bounce=23×24=16 meters
4. Third Bounce: Finally, we calculate the height after the third bounce, which is 23 of the height it reached after the second bounce:
Height after third bounce=23×16=323 meters≈10.67 meters
Thus, the height to which the ball will rise at the third bounce is approximately 10.67 meters.
Height after first bounce=23×36=24 meters
Height after second bounce=23×24=16 meters
Height after third bounce=23×16=323 meters≈10.67 meters
Similar Questions
When a ball bounces, it rises to 23 of the height from which it fell. If the ball is dropped from a height of 36 m, how high will it rise at the third bounce? 1013m (b) 1023m (c) 1213m (d) 1223m
View SolutionWhen a ball bounces, it rises to 34 of the height from which it fell. If the ball is dropped from a height of 32 m, how high will it rise at the third bounce? (a) 13 m (b) 1312 m (c) 1412 m (d) None of these
View Solution
Knowledge Check
- Question 1 - Select One
A ball is dropped from a height of 10 m, as it falls,
Aits velocity increases and acceleration decreases.Bits velocity decreases and acceleration increases.Cits velocity increases and acceleration remains constant.Dits velocity and acceleration remains constant. - Question 2 - Select One
A bouncing tennis ball rebounds each time to a height equal to one half the height of the previous bounce. If it is dropped from a height of 16 m , find the total distance it has travelled when it hits ground for the 10th time :
A471516B37516C671116Dnone of these - Question 3 - Select One
A body is dropped from a height equal to radius of the earth. The velocity acquired by it before touching the ground is
Adirectly proportional to the time of fall.Bdirectly proportional to the square of the time o fall.Cdirectly proportional to mass of the body.DBoth (a) and (c)
A ball is dropped from height 10 m . Ball is embedded in sand 1 m and stops, then
View SolutionA tennis ball is released from height h above ground level. If the ball makes inelastic collision with the ground, to what height will it rise after third collision
View SolutionA tennis ball is released from height h above ground level. If the ball makes inelastic collision with the ground, to what height will it rise after third collision
View SolutionA ball of mass 2kg dropped from a height H above a horizontal surface rebounds to a height h after one bounce. The graph that relates H to h is shown in figure. If the ball was dropped from an initial height of 81 m and made ten bounces, the kinetic energy of the ball immediately after the second impact with the surface was
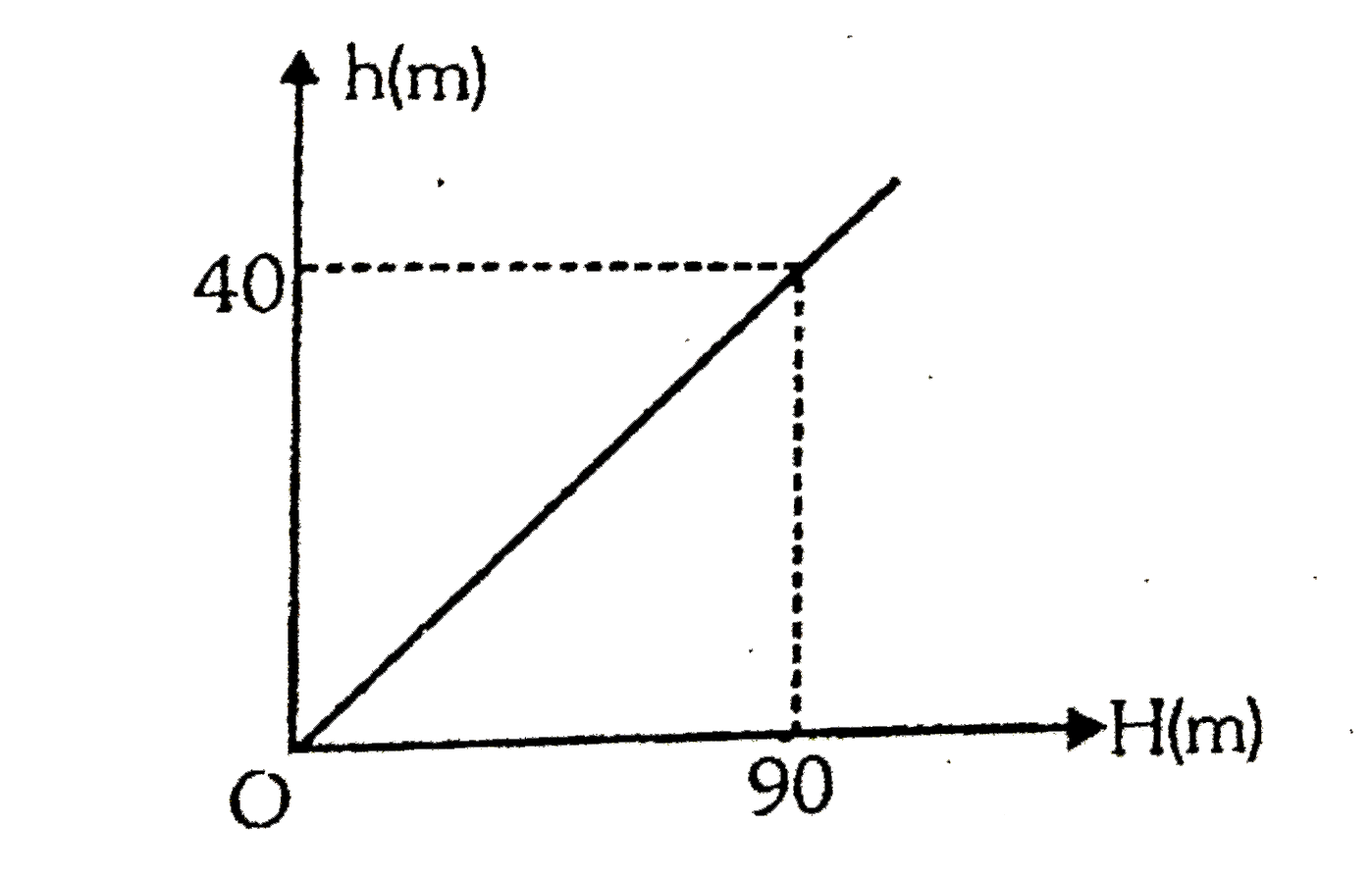 View Solution
View SolutionA metal ball falls from a height of 32 metre on a steel plate. If the coefficient of restitution is 0.5, to what height will the ball rise after second bounce
View Solution

