In a triangle ABC, the sides AB, AC are produced and the bisectors of exterior angles of ∠ABCand∠ACB intersect at D. If ∠BAC=50∘, then ∠BDC is equal to
A)115∘
B)65∘
C)55∘
D)40∘
To solve the problem, we need to find the measure of angle BDC in triangle ABC, given that angle BAC is 50 degrees.
1. Understanding the Triangle and Angles:
- We have triangle ABC with angle BAC = 50 degrees.
- The sides AB and AC are extended, creating exterior angles at B and C.
2. Identifying the Exterior Angles:
- The exterior angle at B is given by:
Exterior angle at B=180∘−∠ABC
- The exterior angle at C is given by:
Exterior angle at C=180∘−∠ACB
3. Using the Angle Bisector Theorem:
- The angle bisector of an exterior angle divides it into two equal parts.
- Let ∠ABC=x and ∠ACB=y.
- By the triangle angle sum property, we know:
∠A+∠B+∠C=180∘
Thus:
50∘+x+y=180∘⟹x+y=130∘
4. Finding the Angles:
- The exterior angle bisector at B will create two angles of:
180∘−x2
- The exterior angle bisector at C will create two angles of:
180∘−y2
5. Finding Angle BDC:
- The angle BDC is formed by the intersection of the two exterior angle bisectors.
- According to the theorem regarding the intersection of exterior angle bisectors:
∠BDC=90∘−∠A2
- Substituting the value of angle A (which is 50 degrees):
∠BDC=90∘−50∘2=90∘−25∘=65∘
Final Answer:
∠BDC=65∘
- We have triangle ABC with angle BAC = 50 degrees.
- The sides AB and AC are extended, creating exterior angles at B and C.
- The exterior angle at B is given by:
Exterior angle at B=180∘−∠ABC
- The exterior angle at C is given by:
Exterior angle at C=180∘−∠ACB
- The angle bisector of an exterior angle divides it into two equal parts.
- Let ∠ABC=x and ∠ACB=y.
- By the triangle angle sum property, we know:
∠A+∠B+∠C=180∘
Thus:
50∘+x+y=180∘⟹x+y=130∘
- The exterior angle bisector at B will create two angles of:
180∘−x2
- The exterior angle bisector at C will create two angles of:
180∘−y2
- The angle BDC is formed by the intersection of the two exterior angle bisectors.
- According to the theorem regarding the intersection of exterior angle bisectors:
∠BDC=90∘−∠A2
- Substituting the value of angle A (which is 50 degrees):
∠BDC=90∘−50∘2=90∘−25∘=65∘
∠BDC=65∘
Similar Questions
If in a ΔABC angle bisectors of exterior angle ∠Band∠C intersect at P ∠BPC=40∘ find ∠A
View SolutionIn △ABC ,∠A=50∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=50∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान क्या होगा ?
View Solution
Knowledge Check
ABC is a triangle. The bisectors of the internal angle ∠B and external angle ∠C Intersect at D. If ∠BDC=50∘, then ∠A is
A100∘B90∘C150∘D30∘In a ΔABC, angle bisector of interior angle B and exterior angle C intersect at P . If ∠A=70∘ . Find ∠BPC.
A25B35C40D45In ΔABC, if AB=AC and ∠B=50∘, then ∠C is equal to
A40∘B50∘C80∘D130∘
In △ABC ,∠A=50∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=50∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान किसके बराबर होगा ?
View SolutionIn △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View SolutionABC is a triangle. The bisectors of the internal ∠B and external ∠C intersect at D. If angle ∠BDC=50˙ , then ∠A is
View SolutionIn figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
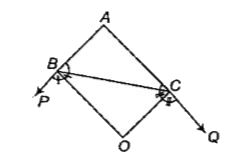
View SolutionThe side BC of ΔABC is produced to D. The bisectors of ∠ABCand∠ABD meet at E. If AB = AC and ∠BEC=24∘. then the measure of ∠ABC is :
View Solution
