The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the triangle CPD ?
24 square cm
15 square cm
12.5 square cm
9.375 square cm
To find the area of triangle CPD in the cyclic quadrilateral ABCD, we can use the relationship between the areas of triangles formed by the diagonals intersecting at point P.
1. Understanding the Given Information:
- Area of triangle APB = 24 cm²
- Length of AB = 8 cm
- Length of CD = 5 cm
2. Using the Property of Similar Triangles:
- Since ABCD is a cyclic quadrilateral, triangles APB and CPD are similar. This is due to the angles subtended by the same arc being equal, and the vertically opposite angles at point P being equal.
3. Setting Up the Ratio of Areas:
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
Area of △APBArea of △CPD=(ABCD)2
4. Substituting the Known Values:
- We know:
Area of △APBArea of △CPD=(85)2
- This simplifies to:
24Area of △CPD=6425
5. Cross-Multiplying to Solve for Area of Triangle CPD:
- Cross-multiplying gives:
24⋅25=64⋅Area of △CPD
- This simplifies to:
600=64⋅Area of △CPD
6. Dividing to Isolate Area of Triangle CPD:
- Now, divide both sides by 64:
Area of △CPD=60064=9.375 cm2
Final Answer:
The area of triangle CPD is 9.375 cm².
- Area of triangle APB = 24 cm²
- Length of AB = 8 cm
- Length of CD = 5 cm
- Since ABCD is a cyclic quadrilateral, triangles APB and CPD are similar. This is due to the angles subtended by the same arc being equal, and the vertically opposite angles at point P being equal.
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
Area of △APBArea of △CPD=(ABCD)2
- We know:
Area of △APBArea of △CPD=(85)2
- This simplifies to:
24Area of △CPD=6425
- Cross-multiplying gives:
24⋅25=64⋅Area of △CPD
- This simplifies to:
600=64⋅Area of △CPD
- Now, divide both sides by 64:
Area of △CPD=60064=9.375 cm2
The area of triangle CPD is 9.375 cm².
Similar Questions
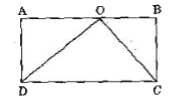
In the figure given above, the area of rectangle ABCD is 100 square cm, O is any point on AB and CD = 20 cm. Then the area of triangle COD ia
View SolutionThe sides AD, BC of a trapezium. ABCD are parallel and the diagonals AC and BD meet at O. If the area of triangle AOB is 3 cm and the area of triangle BDC is 8 cm2, then what is the area of triangle AOD?
View Solution
Knowledge Check
ABCD is a rectangle of perimeter 48 cm with AB = 6 cm and CD = DE .What is the area of the triangle ACE ?
 A18cm2B24cm2C30cm2D36cm2
A18cm2B24cm2C30cm2D36cm2If medians of a triangle have lengths 18 cm, 24 cm and 30 cm, what is the area ( in cm2 ) of the triangle ?
A24√6B244C288D360ABCD is a quadrilateral. The diagonals of ABCD intersect at the point P. The area of the triangles APD and BPC are 27 and 12, respectively. If the areas of the triangles APB and CPD are equal, then the area of triangle APB is
A12B18C15D16
ABCD is a rectangle. The diagonals AC and BD intersect at O. If AB = 32 cm and AD = 24 cm, then what is OD equal to ?
View SolutionIf medians of a triangle have lengths 18 cm, 24 cm and 30 cm, what is the area (in cm2) of the triangle ?
View SolutionIn a triangle ABC, AB = 8 cm, AC = 10 cm and ∠B=90∘, then the area of ΔABC is
View SolutionThe side of an equilateral triangle is equal to the diagonal of the square. If the side of the square is 10 cm, then what is the area of the equilateral triangle?
View SolutionThe side of an equilateral triangle is equal to the diagonal of the square. If the side of the square is 12 cm, then what is the area of the equilateral triangle?
View Solution
