Question

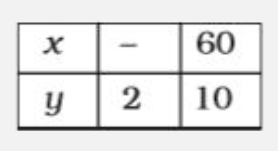
If x varies as y, then which of the following is/are correct?
1. $x^2+y^2$ varies as $x^2-y^2$
2. $\frac{x}{y^2}$ varies inversely as y
3. $\sqrt[n]{n{x}^{2}y}$ varies as $\sqrt[2n]{2n{x}^4{y}^2}$
Select the correct answer using the code given below :

Options

A. 1 and 2 only
B. 2 and 3 only
C. 3 only
D. 1, 2 and 3

Explanation

To solve the problem, we need to analyze each statement given the condition that $$x$$ varies as $$y$$. This means we can express $$x$$ in terms of $$y$$ as follows:

$$x=k\cdot y$$

where $$k$$ is a constant.

Now, let's evaluate each statement one by one.

Statement 1: $$x^2+y^2$$ varies as $$x^2-y^2$$

1. Substitute \( x = k \cdot y \) into both expressions:
- \( x^2 = (k \cdot y)^2 = k^2 y^2 \)
- Therefore, \( x^2 + y^2 = k^2 y^2 + y^2 = (k^2 + 1) y^2 \)
- And \( x^2 - y^2 = k^2 y^2 - y^2 = (k^2 - 1) y^2 \)

2. Now we can see that:
- \( x^2 + y^2 \) varies as \( y^2 \)
- \( x^2 - y^2 \) also varies as \( y^2 \)

3. The ratio of \( x^2 + y^2 \) to \( x^2 - y^2 \) is:
\( \frac{x^2 + y^2}{x^2 - y^2} = \frac{(k^2 + 1) y^2}{(k^2 - 1) y^2} = \frac{k^2 + 1}{k^2 - 1} \)
This is a constant, meaning both expressions vary together.

Conclusion for Statement 1: True

Statement 2: \( \frac{x}{y^2} \) varies inversely as \( y \)

1. Substitute \( x = k \cdot y \):
\( \frac{x}{y^2} = \frac{k \cdot y}{y^2} = \frac{k}{y} \)

2. This shows that \( \frac{x}{y^2} \) varies inversely as \( y \).

Conclusion for Statement 2: True

Statement 3: \( \sqrt(n){x^2y} \) varies as \( \sqrt(2n){x^4y^2} \)

1. Substitute \( x = k \cdot y \):
- \( x^2 = k^2 y^2 \)
- Therefore, \( x^2y = k^2 y^2 \cdot y = k^2 y^3 \)
- Thus, \( \sqrt(n){x^2y} = \sqrt(n){k^2 y^3} = \sqrt(n){k^2} \cdot y^{3/n} \)

2. Now for \( \sqrt(2n){x^4y^2} \):
- \( x^4 = (k^2 y^2)^2 = k^4 y^4 \)
- Therefore, \( x^4y^2 = k^4 y^4 \cdot y^2 = k^4 y^6 \)
- Thus, \( \sqrt(2n){x^4y^2} = \sqrt(2n){k^4} \cdot y^{6/(2n)} = \sqrt(2n){k^4} \cdot y^{3/n} \)

3. Both expressions contain \( y^{3/n} \) and differ only by constants:
- \( \sqrt(n){k^2} \) and \( \sqrt(2n){k^4} \) are constants.

Conclusion for Statement 3: True

Final Conclusion:
All three statements are true.

Summary of Steps:
1. Analyze the relationship between \( x \) and \( y \) using the proportionality condition.
2. Substitute \( x = k \cdot y \) into each statement.
3. Simplify the expressions and check if they vary together or inversely.
4. Conclude the truth of each statement based on the analysis.