The number of items in a booklet is N. In the first year there is an increase of x% in this number and in the subsequent year there is a decrease of x%. At the end of the two years, what will be the number of items in the booklet ?
Less than N
Equal to N
More than N
It depends on the value of N
To solve the problem step by step, we will first define the variables and then apply the formula to find the final number of items after the two years.
1. Define the Initial Variables:
- Let N be the initial number of items in the booklet.
- Let x be the percentage increase in the first year and the percentage decrease in the second year.
2. Calculate the Number of Items After the First Year:
- In the first year, the number of items increases by x%.
- The formula for the new number of items after the increase is:
N1=N+(x100×N)=N(1+x100)
3. Calculate the Number of Items After the Second Year:
- In the second year, the number of items decreases by x% from the new total N1.
- The formula for the new number of items after the decrease is:
N2=N1−(x100×N1)=N1(1−x100)
- Substituting N1 from the previous step:
N2=N(1+x100)(1−x100)
4. Simplify the Expression:
- We can use the difference of squares to simplify:
N2=N(1−(x100)2)
- This means that the final number of items after two years is:
N2=N(1−x210000)
5. Conclusion:
- The final number of items in the booklet after two years is:
N2=N(1−x210000)
- This shows that the final number of items is less than the initial number N as long as x is positive.
- Let N be the initial number of items in the booklet.
- Let x be the percentage increase in the first year and the percentage decrease in the second year.
- In the first year, the number of items increases by x%.
- The formula for the new number of items after the increase is:
N1=N+(x100×N)=N(1+x100)
- In the second year, the number of items decreases by x% from the new total N1.
- The formula for the new number of items after the decrease is:
N2=N1−(x100×N1)=N1(1−x100)
- Substituting N1 from the previous step:
N2=N(1+x100)(1−x100)
- We can use the difference of squares to simplify:
N2=N(1−(x100)2)
- This means that the final number of items after two years is:
N2=N(1−x210000)
- The final number of items in the booklet after two years is:
N2=N(1−x210000)
- This shows that the final number of items is less than the initial number N as long as x is positive.
Similar Questions
If in the population of a town there is an increase of 44% in the first year and 75% in the second year,then what is the average rate of increase in the population?
View SolutionThe population of a village is 10000. If the population increase by 10% in the first year, by 20% in the second year and due to mass exodus it decreases by 5% in the third year, what will be its population after 3 years
View Solution
Knowledge Check
- Question 1 - Select One
If the population of a town increases by 25% in the first year and increases by 36% in the second year, then what is the average rate (in percentage) of increase in the population?
A0.45B0.595C0.74D0.76 - Question 2 - Select One
Select the most appropriate word to Fill in the blank.
Last Year there was an increase ______ the number of road a ccidents on the Eastern Expressway.AatBtoCinDwith - Question 3 - Select One
An institute has 2500 members. If it increases 10% in the first year and decreases 10% in the second year, what will be the increment or decrement in the number of members after these two years?
ANo increase no decreaseBIncrease of 25 membersCDecrease of 25 membersDNone of the above
The population of a variety of tiny bush in an experimental field increased by 10% in the first year, increased by 8% in the second year but decreased by 10% in the third year. If the present number of bushes in the experimental field is 26730, then the number of bushes in the beginning was 25000 b. 27000 c. 28000 d. 24600
View Solution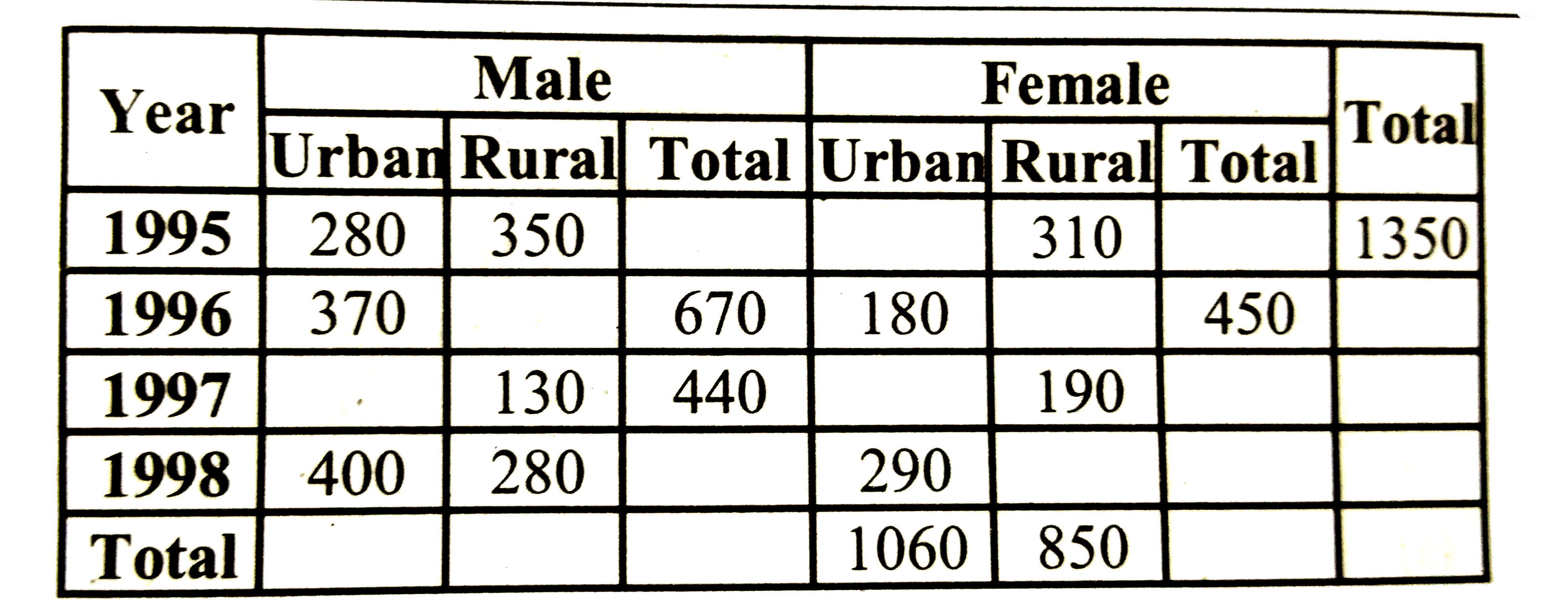
What is the difference between the number of females and the number of males in the year 1995?View SolutionThe population of a town is 198000. It decreases by 8% in the first year and increases by 5% in the second year What is the population of the town at the end of 2 years?
View Solution2000 employees are assigned to complete a project. At the endofthefirst year, 15% of the number of employees are decreased and at the end of the second year again 10% of the number of employees are decreased. However, to complete the project in time, the number of employees are increased by 10% at the end ofthe third year. What was the number of employees working during the fourth year?
View SolutionThe population of a variety of tiny bush in an experimental field increased by 10% in the first year, increased by 8% in the second year but decreased by 10% in the third year. If the present number of bushes in the experimental field is 26730, then the number of bushes in the beginning was 25000 b. 27000 c. 28000 d. 24600
View Solution

