In a ΔABC, AC = 12 cm, AB = 16 cm and AD is the bisector of ∠A. If BD = 4 cm, then what is DC equal to ?
2 cm
3 cm
4 cm
5 cm
To find the length of segment DC in triangle ABC where AD is the angle bisector of angle A, we can apply the Angle Bisector Theorem. The theorem states that the ratio of the lengths of the two segments created by the angle bisector is equal to the ratio of the lengths of the other two sides of the triangle.
Given:
- AC = 12 cm
- AB = 16 cm
- BD = 4 cm
- Let DC = x cm
1. Apply the Angle Bisector Theorem:
According to the Angle Bisector Theorem:
ABAC=BDDC
2. Substitute the known values:
We know that:
- AB = 16 cm
- AC = 12 cm
- BD = 4 cm
- DC = x cm
Substituting these values into the equation gives:
1612=4x
3. Cross-multiply to solve for x:
Cross-multiplying gives:
16x=12⋅4
16x=48
4. Divide both sides by 16:
x=4816
x=3
5. Conclusion:
Therefore, the length of segment DC is:
DC=3 cm
Final Answer:
DC = 3 cm
- AC = 12 cm
- AB = 16 cm
- BD = 4 cm
- Let DC = x cm
According to the Angle Bisector Theorem:
ABAC=BDDC
We know that:
- AB = 16 cm
- AC = 12 cm
- BD = 4 cm
- DC = x cm
1612=4x
Cross-multiplying gives:
16x=12⋅4
16x=48
x=4816
x=3
Therefore, the length of segment DC is:
DC=3 cm
DC = 3 cm
Similar Questions
Knowledge Check
In ΔABC,AB=5cm,AC=7cm. If AD is the angle bisector of ∠A Then BD:CD is :
A25:49B49:25C6:1D5:7In a ΔABC, BC = 9 cm, AC = 40 cm and AB = 41 cm. If bisector of angle A meets side BC at D then ratio of area of ΔABD and ΔABC is
A41:40B9:40C9:41D41:81In a △ABC. AB = 5 cm, AC = 7 cm. If AD is the angle bisector of angle A, then BD :CD is :
A25:49B49:25C6:1D5:7
In △ABC, AB=7 cm, BC = 10 cm, and AC = 8 cm. If AD is the angle bisector of ∠BAC , where D is a point on BC, then BD is equal to:
View SolutionIn ΔABC,AB=12cm,BC=16cm and CA=20cm If D is the mid point of AC then the length of BD is
View SolutionIn a ΔABC,AB=5cm,AC=5cmandangleA=50∘, then ∠B=
View SolutionIn ΔABC,AD is the inernal besector of ∠A. If BD = 5cm , BC=7.5 cm , then AB:AC=
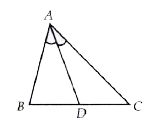
View SolutionIn figure AD is the bisector of ∠BAC. If BD=2cm,CD=3cmandAB=5cm. Find AC :

View Solution