To a circle with centre at 0, two tangents AP and AQ are drawn from an external point A. If the ∠PAQ = 80∘, then the ∠POQ is:
80∘
70∘
90∘
100∘
The correct Answer is:D
To solve the problem, we will follow these steps:
1. Understanding the Geometry: We have a circle with center O, and two tangents AP and AQ drawn from an external point A. The angle PAQ is given as 80 degrees.
2. Identifying Right Angles: Since AP and AQ are tangents to the circle, they meet the radius at points P and Q at right angles. Therefore, we have:
- Angle AOP = 90 degrees
- Angle AOQ = 90 degrees
3. Setting Up the Angles: The angles around point A can be expressed as:
- Angle PAQ + Angle AOP + Angle AOQ + Angle POQ = 360 degrees
- Substituting the known values, we have:
- 80 degrees + 90 degrees + 90 degrees + Angle POQ = 360 degrees
4. Calculating Angle POQ: Now, we can simplify the equation:
- 80 + 90 + 90 + Angle POQ = 360
- 260 + Angle POQ = 360
- Angle POQ = 360 - 260
- Angle POQ = 100 degrees
Thus, the angle POQ is 100 degrees.
Summary of Steps:
1. Recognize the properties of tangents and the circle.
2. Identify the right angles formed by the tangents and the radius.
3. Set up the equation for the angles around point A.
4. Solve for the unknown angle POQ.
- Angle AOP = 90 degrees
- Angle AOQ = 90 degrees
- Angle PAQ + Angle AOP + Angle AOQ + Angle POQ = 360 degrees
- Substituting the known values, we have:
- 80 degrees + 90 degrees + 90 degrees + Angle POQ = 360 degrees
- 80 + 90 + 90 + Angle POQ = 360
- 260 + Angle POQ = 360
- Angle POQ = 360 - 260
- Angle POQ = 100 degrees
1. Recognize the properties of tangents and the circle.
2. Identify the right angles formed by the tangents and the radius.
3. Set up the equation for the angles around point A.
4. Solve for the unknown angle POQ.
Similar Questions
A circle is centered at O. Two tangents AP and AQ are drawn from an external point A. If ∠POQ=118∘, then the ∠PAQ is:
एक वृत्त O पर केंद्रित है। दो स्पर्श रेखाएं AP और AQ बाह्य बिंदु A से खींचे गए हैं। यदि ∠POQ=118∘, फिर ∠PAQ = ?View SolutionIf two tangent TP and TQ are drawn from an external point T such that ∠TQP=60∘ then find ∠OPQ.
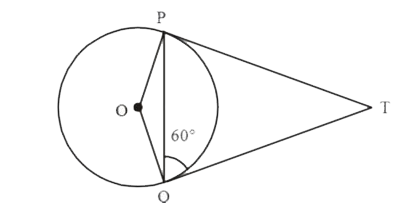 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two tangents PA and PB are drawn to a circle with centre O from an external point P. If ∠OAB=30∘, then ∠APB is:
केंद्र O वाले वृत्त पर एक बाहरी बिंदु P से दो स्पर्श रेखाएँ PA तथा PB खींची जाती हैं | यदि ∠OAB=30∘ है, तो ∠APB का मान क्या होगा ?A15∘B30∘C120∘D60∘
Two tangents AP and AQ are drawn to a circle with centre O from an external point A, where P and Q are points on the circle. If the ∠PAQ=70∘, then the ∠AOP is equal to:
दो स्पर्शरेखा AP और AQ एक बाहरी बिंदु A से केंद्र O के साथ एक वृत्त में खींची जाती हैं, जहां P और Q वृत्त पर बिंदु होते हैं। यदि ∠PAQ=70∘, तो ∠AOP का मान है:View Solutiontwo tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR= PR+ RQ
View SolutionFrom the external point P tangents PA and PB are drawn to a circle with centre O. If ∠PAB=50∘, then find ∠AOB.
View SolutionTheorem: The length of two tangents drawn from an external point to a circle are equal.
View SolutionProve that the lengths of tangents drawn from an external point to a circle are equal.
View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠APB=2∠OAB
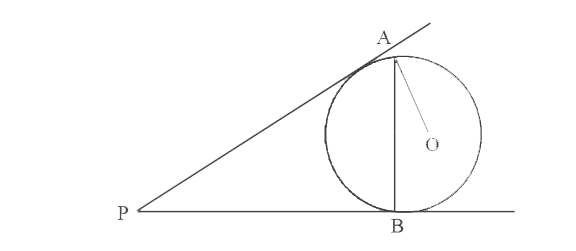 View Solution
View SolutionThe lengths of tangents drawn from an external point to a circle are ________.
View Solution

