In a Radioactive decay $A k_{1} - - \to B k_{2} - - \to C (K_{1} > K_{2})$
Initially B is not present, then correct curve for centration of B with respect to time is

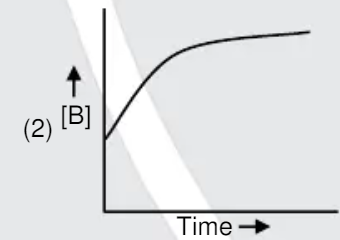
ocr_image

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of determining the correct curve for the concentration of B with respect to time during the radioactive decay process $A_{1} B_{2} C$ , we can follow these steps:
Step 1: Understand the decay process
In this process, substance A decays into substance B at a rate $k_{1}$ , and substance B decays into substance C at a rate $k_{2}$ . Given that $k_{1} > k_{2}$ , this indicates that B is formed more rapidly than it is converted into C.
Step 2: Analyze the initial conditions
Initially, the concentration of B is zero. As time progresses, B will begin to form as A decays. Since $k_{1}$ is greater than $k_{2}$ , B will accumulate quickly at first.
Step 3: Determine the behavior of B over time
- Formation of B: Since $k_{1}$ is larger, the concentration of B will rise rapidly as A decays.
- Decomposition of B: However, B will also start to decay into C, but at a slower rate because $k_{2}$ is smaller than $k_{1}$ . This means that while B is being formed quickly, it will not decompose as quickly.
Step 4: Sketch the concentration curve
1. Initial Phase: At time $t = 0$ , the concentration of B is zero.
2. Increasing Phase: As time progresses, the concentration of B increases rapidly due to the faster formation from A.
3. Plateau Phase: Eventually, the rate of formation of B will start to balance out with the rate of its decay into C, leading to a slower increase and then a plateau.
4. Decreasing Phase: After reaching a maximum, the concentration of B will begin to decrease slowly as it decays into C.
Step 5: Identify the correct graph
Based on the analysis, the correct graph will show:
- A rapid increase in the concentration of B initially.
- A gradual leveling off as it reaches a maximum.
- A slow decrease after reaching the peak.
This behavior matches with Option 1 from the given choices.
Final Answer:
The correct curve for the concentration of B with respect to time is represented by Option 1.
---

Updated on:18/9/2024

For a reaction scheme $A k_{1} - - \to B k_{2} - - \to C$ , if the rate of formation of B is set to be zero then the concentration of B is given by :
A $(k_{1} + k_{2}) [A]$
B $(k_{1} + k_{2}) [A]$
C $k_{1} k_{2} [A]$
D $(\frac{k_{1}}{k_{2}}) [A]$
In the given sequence of first order reaction,
$A k_{1} - - \to B k_{2} - - \to k_{3} - - \to D$
What is the ratio of numbers of atoms of A to the number of atoms of B after long time interval starting with pure A, where $k_{1}$ where $K_{1}$ $k_{1} = \frac{I n 2}{20 \times 60}, k_{2} = \frac{I n 2}{30} ?$
A $\frac{2}{3}$
B $10$
C $20$
D $40$
Statement -1: In $A k_{1} - - \to B k_{2} - - \to C$
If half life of A is very less as compared to B, then, net reaction is A to C with rate constant $(k_{1} \times k_{2})$
Statement-2: Slowest step is the rate determining step si B to C is rate determining step.
AStatement-1 is True, statement-2 is True, Statement-2 is a correct explantion for Statement-1.
BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1
CStatement-1 is True, Statement-2 is False.
DStatement-1 is False, Statement-2 is True.