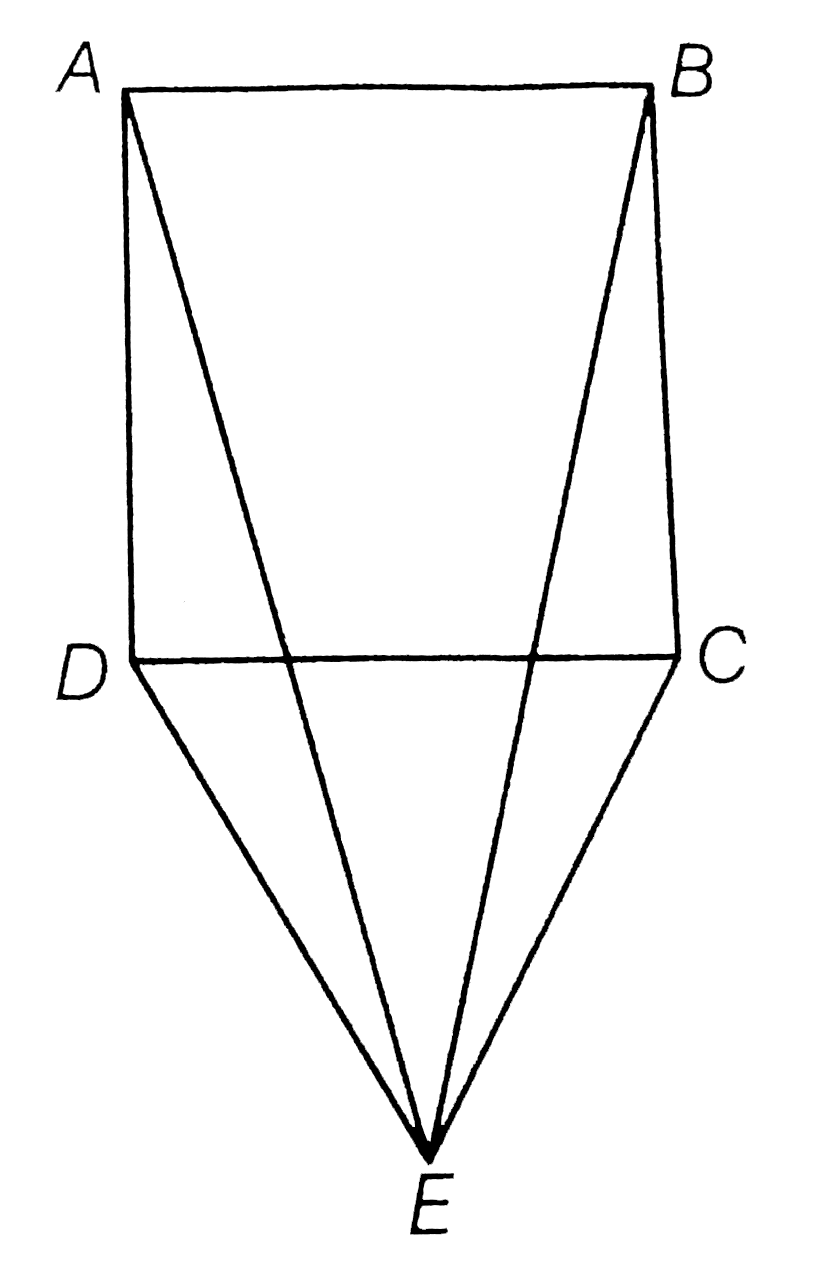
Inside a square ABCD, ΔBEC is an equilateral triangle. If CE and BD interesect at O, then ∠BOC is equal to
60∘
75∘
90∘
120∘
The correct Answer is:B
To solve the problem, we need to find the angle ∠BOC where O is the intersection of the diagonals CE and BD in the square ABCD with the equilateral triangle ΔBEC.
1. Identify the Angles in the Square:
- In square ABCD, each angle is 90∘.
- Therefore, ∠ABC=90∘.
Hint: Remember that all angles in a square are right angles.
2. Identify the Angles in the Equilateral Triangle:
- In triangle BEC, since it is an equilateral triangle, all angles are equal to 60∘.
- Thus, ∠EBC=60∘ and ∠ECB=60∘.
Hint: In an equilateral triangle, all angles are equal and sum up to 180∘.
3. Determine the Angle ∠DBC:
- Since BD is a diagonal of the square, it bisects ∠ABC.
- Therefore, ∠DBC=12×90∘=45∘.
Hint: The diagonal of a square bisects the angles at the vertices.
4. Apply the Triangle Angle Sum Property:
- In triangle BOC, the sum of the angles must equal 180∘.
- We know ∠DBC=45∘ and ∠EBC=60∘.
- Let ∠BOC=x.
Hint: The sum of angles in any triangle is 180∘.
5. Set Up the Equation:
∠BOC+∠DBC+∠EBC=180∘
x+45∘+60∘=180∘
6. Solve for x:
x+105∘=180∘
x=180∘−105∘=75∘
Hint: Isolate the variable to find its value.
7. Conclusion:
- Therefore, ∠BOC=75∘.
Final Answer:
The angle ∠BOC is equal to 75∘.
- In square ABCD, each angle is 90∘.
- Therefore, ∠ABC=90∘.
- In triangle BEC, since it is an equilateral triangle, all angles are equal to 60∘.
- Thus, ∠EBC=60∘ and ∠ECB=60∘.
- Since BD is a diagonal of the square, it bisects ∠ABC.
- Therefore, ∠DBC=12×90∘=45∘.
- In triangle BOC, the sum of the angles must equal 180∘.
- We know ∠DBC=45∘ and ∠EBC=60∘.
- Let ∠BOC=x.
∠BOC+∠DBC+∠EBC=180∘
x+45∘+60∘=180∘
x+105∘=180∘
x=180∘−105∘=75∘
- Therefore, ∠BOC=75∘.
The angle ∠BOC is equal to 75∘.
Similar Questions
Knowledge Check
- Question 1 - Select One
Inside a square ABCD, ΔBEC is an equilateral triangle. If CE and BD interesect at O, then ∠BOC is equal to
A60∘B75∘C90∘D120∘ - Question 2 - Select One
ABCD is a square. BEC is an equilateral triangle inside the square. If CE & BD intersects at O. Find ∠BOC=?
A60∘B75∘C90∘D120∘ - Question 3 - Select One
In the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
 ARHSBSSSCAASDSAS
ARHSBSSSCAASDSAS
In Figure, ABC is an equilateral triangle. Find m ∠BEC
View SolutionO is a point in the interior of a square ABCD such that ΔOAB is an equilateral triangle . Show that ΔOCD is an isoceles triangle .
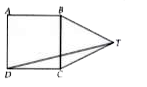
View SolutionIn the given figure, ABCD is a square and ΔBCT is an equilateral triangle. Find ∠BTD.
 View Solution
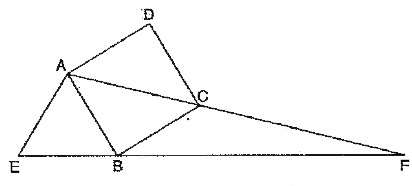
View SolutionABCD is a square, and ABE is an equilateral triangle. ACandEB are produced to meet at F. Calculate the angles of ΔABF.
 View Solution
View SolutionABCD is a square and ABE is an equilateral triangle outside the square then
View Solution

