A particle is moving along x-axis with velocity 40 m/s. It breaks into two parts in mass ratio 1:2. If speed of smaller part is 60 m/s along x-axis then find fractional changes in kinetic energy of system.
18
37
16
25
To solve the problem, we will follow these steps:
Step 1: Define the masses of the two parts
Let the total mass of the original particle be 3m (since the mass ratio is 1:2). Therefore, the masses of the two parts after the break will be:
- Smaller part: m
- Larger part: 2m
Step 2: Calculate the initial kinetic energy
The initial velocity of the particle is 40m/s. The initial kinetic energy (KEi) can be calculated using the formula:
KEi=12mv2
Substituting the values:
KEi=12⋅3m⋅(40)2=12⋅3m⋅1600=2400mJ
Step 3: Determine the velocity of the larger part
We know the speed of the smaller part is 60m/s. To find the speed of the larger part, we can use the conservation of momentum. The initial momentum of the system is:
Initial momentum=(3m)⋅40=120m
After the break, the momentum is given by:
Final momentum=m⋅60+2m⋅v
Setting the initial momentum equal to the final momentum:
120m=m⋅60+2m⋅v
Dividing through by m (assuming m≠0):
120=60+2v
Solving for v:
2v=120−60=60⟹v=30m/s
Step 4: Calculate the final kinetic energy
Now we can calculate the final kinetic energy (KEf):
KEf=12m(60)2+12(2m)(30)2
Calculating each term:
KEf=12m⋅3600+12⋅2m⋅900
KEf=1800m+900m=2700mJ
Step 5: Calculate the change in kinetic energy
The change in kinetic energy (ΔKE) is given by:
ΔKE=KEf−KEi=2700m−2400m=300mJ
Step 6: Calculate the fractional change in kinetic energy
The fractional change in kinetic energy is given by:
Fractional change=ΔKEKEi=300m2400m=18
Final Answer
The fractional change in kinetic energy of the system is 18.
---
Let the total mass of the original particle be 3m (since the mass ratio is 1:2). Therefore, the masses of the two parts after the break will be:
- Smaller part: m
- Larger part: 2m
The initial velocity of the particle is 40m/s. The initial kinetic energy (KEi) can be calculated using the formula:
KEi=12mv2
Substituting the values:
KEi=12⋅3m⋅(40)2=12⋅3m⋅1600=2400mJ
We know the speed of the smaller part is 60m/s. To find the speed of the larger part, we can use the conservation of momentum. The initial momentum of the system is:
Initial momentum=(3m)⋅40=120m
After the break, the momentum is given by:
Final momentum=m⋅60+2m⋅v
Setting the initial momentum equal to the final momentum:
120m=m⋅60+2m⋅v
Dividing through by m (assuming m≠0):
120=60+2v
Solving for v:
2v=120−60=60⟹v=30m/s
Now we can calculate the final kinetic energy (KEf):
KEf=12m(60)2+12(2m)(30)2
Calculating each term:
KEf=12m⋅3600+12⋅2m⋅900
KEf=1800m+900m=2700mJ
The change in kinetic energy (ΔKE) is given by:
ΔKE=KEf−KEi=2700m−2400m=300mJ
The fractional change in kinetic energy is given by:
Fractional change=ΔKEKEi=300m2400m=18
The fractional change in kinetic energy of the system is 18.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
A block moving horizontally on a smooth surface with a speed of 40 m/s splits into two parts with messes in the ratio of 1:2 If the smaller part moves at 60 m/s in the same direction , then fractional change in kinetic energy is :
View SolutionA particle of mass m is moving along the x-axis with initial velocity u i . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
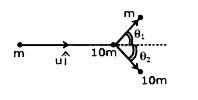
View Solution
Knowledge Check
For a particle moving along the x-axis, mark the correct statement(s).
Aif x is positive and is increasing with the time, then average velocity of the particle is positive.Bif x is negative and becoming positive after some time, then the velocity of the particle is always positive.CIf x is negative and becoming less negative as time passes, then the average velocity of the particle is positive.DIf x is positive and is increasing with time, then the velocity of the particle is always positive.A space craft of mass M is travelling in space with velocity v. It then breaks up into two parts such that the smaller part m comes to the rest, then the velocity of the remaining part is-
AMvM−mBMvM+mCmvM−mDMvmA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
A8 m/sB16 m/sC4 m/sD0 m/s
Initially a body of mass 10kg is moving along x-axis with velocity 10√3 m/s. It collides with another body of mass 20kg and comes to rest. The 20kg mass object disintegrates in 2 parts each of mass 10kg. One part moves along y-axis with velocity 10m/s and another at 30 degrees with x-axis. Evaluate velocity of object which moves at angle 30 degrees with x-axis
View SolutionA particle is moving along X -axis with 4m/s. in front of plane mirror which is moving along , negative direction with [2m/s .Speed of image , with respect to ground will be:
View SolutionA big particle of mass (3+m) kg blasts into 3 pieces , such that a particle of mass 1 kg moves along x - axis , with velocity 2ms−1 and a particle of mass 2 kg moves with velocity 1ms−1 perpendicular to direction of 1 kg particle . If the third particle moves with velocity √2ms−1, then m is
View SolutionA particle is moving along a straight line along x-zxis with an initial velocity of 2m/s towards positive x-axis. A constant acceleration of 0.5m/s2 towards negative x-axis starts acting on particle at t=0. Find velocity (in m/s) of particle at t=2s.
View SolutionA particle moves along x-axis with acceleration a=6(t−1) where t is in second. If the particle is initially at the origin and it moves along positive x-axis with v0=2m/s, find the nature of motion of the particle.
View Solution
